Abstract

  1. Introduction

    1.1 Periodic auction and continuous limit order book

    1.2 Comparison and main flaws of limit order book

    1.3 Optimal policies to cure auction’s inefficiencies and related works

  2. Auctions market modeling with transaction fees and randomization

    2.1 The market characteristics

    2.2 Clearing Price rule

    2.3 Strategic Trader’s optimization and market quality

    2.4 Data and numerical analysis

    2.5 Strategic trader with full information: efficient but unfair market

    2.6 Imperfect information and inefficiency of auctions

  3. Monitoring policies: transaction fees and clearing time randomization

    3.1 Bilevel optimization between the exchange and the strategic trader

    3.2 Randomization without fees

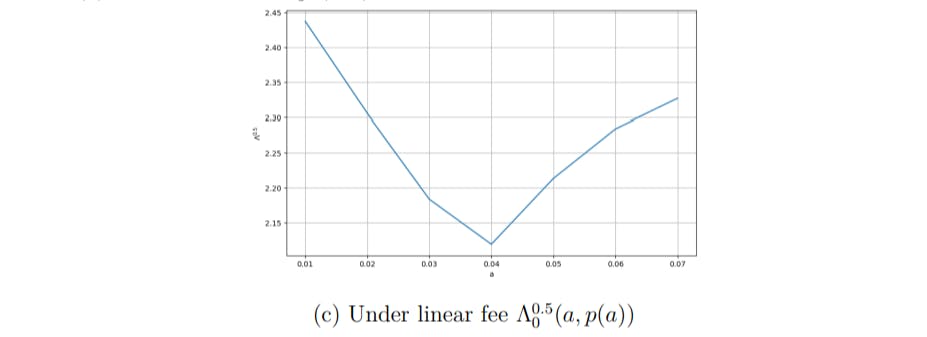
    3.3 Optimal transaction fees indexed on time to improve price impact for the trader

    3.4 Optimal transaction fees indexed on time: improving market quality while benefiting from the fees

  4. Conclusions

A. Appendix: Numerical Methods

A.1 Problem of a Strategic Seller

A.2 Appendix: Problem of the Regulator

B Appendix: Illustrate Remark 2.4

References

4 Conclusions

We study the strategic arrival of a trader and show that a strategic trader always joins an auction at the last moment to have the greatest price manipulation power. Such behavior could impair fairness and market quality especially if the trader has a misconception of the efficient price. We propose two solutions: randomizing the closing time and introducing time-dependent transaction fees. With randomization (91% of chance auction closes at T = 10 and 9% of chance closes at T = 9), the strategic trader would join the auction before the last moment and market quality is improved. With transaction fees, the strategic trader would enter the auction even earlier which further improves the market quality. We consider two possible interests of the exchange, improving the market quality and making fee gains. Under either considerations, our solution provides better results than without randomization or fees.

Our results certainly have limitations. We assume the presence of a single strategic trader instead of allowing multiple strategic traders to compete. In terms of model setting, [Gayduk and Nadtochiy (2020)] studies a general optimal control and stopping problem with discrete controls and proves the existence of an equilibrium in a game in which every player is strategic, without studying randomization or transaction fees policy. Our paper is a specific optimal control and stopping problem with discrete stopping time and we assume all but one players are non-strategic. [Gayduk and Nadtochiy (2020)] sheds light on a possible extension of our model to a more general case when there are more than one strategic players in an auction. [Alfonsi and Blanc (2016)] studies the optimal execution strategy of a strategic trader in a continuous market whose order has price impact on the market and finds that the existence of price manipulation strategies depend on the choice of models. This reminds us that changing certain settings of our model may change the behavior of the strategic trader and possibly our conclusion. Updating the model to include interactions of multiple strategic traders would probably lead to similar results of this paper. Strategic traders would very likely still choose to arrive at the last moment to avoid sharing their views too early and to gain information of others to take advantage. We also assume a discrete optimal stopping control instead of a continuous one. The continuous version of this problem is in the works. We assume the auction market clears all order imbalance while in reality order imbalance exists. Finding a workable model to allow order imbalance is a future direction to consider. In addition, we model simply one round of an auction. If running the auction for several rounds, we could possibly see a larger negative impact of the strategic trader’s arrival-timing strategy and see a greater need to regulate the arrival of traders.

Finally, we did not mention priority rules for a periodic auction. This is because our model assumes zero imbalance of orders, so we do not find the need of a priority rule. In reality, order imbalance exists; for example, if A wants to sell 10 shares of stock, B wants to buy 4 shares of stock, and C wants to buy 8 shares of stock, B or C or both might only receive part of what they request. Priority rules need to be set to divide the 10 shares in this situation. Cboe’s periodic auction market assigns price priority over size priority over time priority; [Budish et al. (2015)] also mentions that price priority should be given over time priority. In general, time priority should be the last to consider. Therefore, we argue that our observation (a strategic trader lacks an incentive to join early) would still be valid given the presence of order imbalance and priority rules. However, learning how to set priority rules for order imbalance could be a meaningful future study.

Authors:

(1) Thibaut Mastrolia, UC Berkeley, Department of Industrial Engineering and Operations Research ([email protected]);

(2) Tianrui Xu, UC Berkeley, Department of Mathematics ([email protected]).

This paper is available on arxiv under CC BY 4.0 DEED license.