A Radical Neural Network Approach to Modeling Shock Dynamics

Table of Links

Abstract and 1. Introduction

1.1. Introductory remarks

1.2. Basics of neural networks

1.3. About the entropy of direct PINN methods

1.4. Organization of the paper

2. Non-diffusive neural network solver for one dimensional scalar HCLs

   2.1. One shock wave

   2.2. Arbitrary number of shock waves

   2.3. Shock wave generation

   2.4. Shock wave interaction

   2.5. Non-diffusive neural network solver for one dimensional systems of CLs

   2.6. Efficient initial wave decomposition

3. Gradient descent algorithm and efficient implementation

   3.1. Classical gradient descent algorithm for HCLs

   3.2. Gradient descent and domain decomposition methods

4. Numerics

   4.1. Practical implementations

   4.2. Basic tests and convergence for 1 and 2 shock wave problems

   4.3. Shock wave generation

   4.4. Shock-Shock interaction

   4.5. Entropy solution

   4.6. Domain decomposition

   4.7. Nonlinear systems

5. Conclusion and References

Abstract

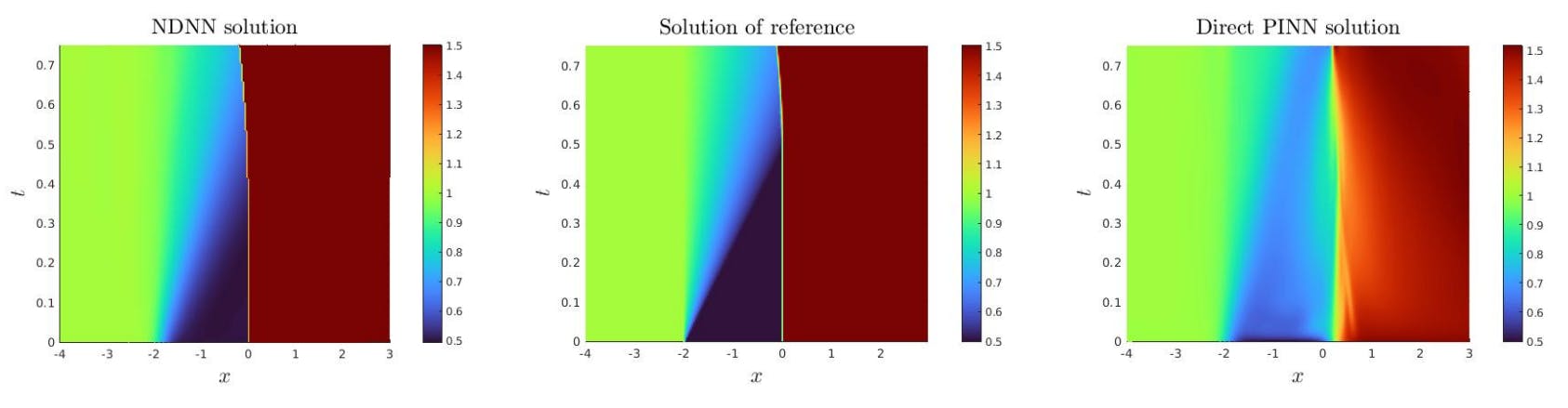
In this paper, we develop a non-diffusive neural network (NDNN) algorithm for accurately solving weak solutions to hyperbolic conservation laws. The principle is to construct these weak solutions by computing smooth local solutions in subdomains bounded by discontinuity lines (DLs), the latter defined from the Rankine-Hugoniot jump conditions. The proposed approach allows to efficiently consider an arbitrary number of entropic shock waves, shock wave generation, as well as wave interactions. Some numerical experiments are presented to illustrate the strengths and properties of the algorithms.

1. Introduction

In this paper we propose to develop a non-diffusive neural network (NDNN) solver for the accurate computation of shock waves in nonlinear (quasi-linear) hyperbolic conservation laws (HCLs). The objective is to track sharply entropic shocks and to circumvent a well-known issue when approximating HCL with Physics informed neural network (PINN) methods, more specifically when approximating shock waves with neural networks. We consider the following Initial Value Problem (IVP):

In addition for Ω bounded, we impose boundary conditions for incoming characteristics, see for instance [1, 2]. We refer [3, 4, 5] for the analysis of HCLs, and to [2, 6, 7] for their standard numerical approximation using finite volume/difference methods.

In this paper, we do not consider non-convex flux functions. The latter is known to generate non-classical shocks, see [4]. However ideas similar to those developed in this paper could be developed for entropic non-classical shocks, by combining piecewise smooth functions and Rankine-Hugoniot solvers (as in the convex case for first order ODE), and additional equations derived from the weak formulation of the PDE specific to non-convex flux [8].

1.1. Introductory remarks

We recall that PINN algorithms allow for the computation of solutions to partial differential equations (PDE), and corresponding inverse problems, by using parameterized neural networks. More specifically, the solution u is approximated by a parameter-dependent network N, and the L 2 -norm (other norms can be used) of the residual of the equation applied to N is minimized by standard (stochastic) gradient descent-type methods. One of the main strengths of this approach, which was originally developed in its most simple form by Lagaris [9], is the use of automatic differentiation of explicit neural networks. There is no need for approximating differential operators, hence avoiding to a certain extent stability issues for evolution PDE. The computation of direct and inverse PDE problems with neural networks has become a very active research area from the practical, numerical as well mathematical points of view. Notice however that a full mathematical analysis of convergence, accuracy and stability is still far from complete. We refer to [10, 11, 12] for details. Notice hereafter that other types of neural network-based algorithms have been developed, see [13, 14, 15].

The approximation of shock waves using direct PINN [10] algorithms can be inaccurate/very diffusive, or even simply not convergent [16]. Among recent papers devoted to the numerical computation of HCL using neural networks, let us mention [17] where is proposed a physics-informed attention-based neural network (PIANN) for non-convex fluxes generating non-classical shock waves [4]. As in our work here, the neural networks in [17] are designed to include some knowledge of the structure of the solution. In [18] is proposed a least squares space-time control volume scheme, using space-time integral form with strong connection with finite volume methods.

By default, neural networks are constructed using smooth activation functions, which precludes the construction of weak discontinuous waves. However, one has the freedom to choose also non-differentiable (ReLU, for instance) activation functions. In this case, the direct application of PINN leads to differentiating a non-smooth function. We note that ReLU functions could be used as the activation function, as long as the training points do not coincide with the points where ReLU functions are not differentiable. However, the main issue in approximating shock waves, comes from that as weak solutions, shock waves are described mathematically from a weak formulation (leading to Rankine-Hugoniot jump conditions), hence independently of the regularity of the chosen activation function. In conclusion, we do not claim that it is impossible to use ReLU functions, but it should be done very carefully and a priori, on the weak formulation of the PDE. In addition, for complex solutions containing several waves (shocks, rarefactions) the convergence of the loss function is difficult to achieve. Notice however that the approximation of rarefaction can usually be accurately performed using deep and complex enough networks.

In the present paper, the proposed approach is focused on the accurate approximation of shock waves. It allows for the generation of shock waves, as well as shock-shock or rarefaction-shock interactions. The principle of the proposed methodology is: i) to use space-time dependent neural networks to solve HCLs in space-time subdomains bounded by curves of discontinuities; ii) use time-dependent neural networks to identify the discontinuity lines (DLs), iii) solve HCL in space-time subdomains where the corresponding solutions are smooth and identify the DLs by minimizing a loss functional measuring the HCL residual in all subdomains and Rankine-Hugoniot’s jump conditions on all the DLs.

More specifically, we decompose the global space-time domain Q in subdomains, which are delimited by the DLs defining shock waves which initially are unknown. The solution in each subdomain, which are bounded by the DLs, and the DLs are then represented by dedicated neural networks. The networks are trained by minimizing a loss functional, which measures the error of the PDE (1a) in each subdomain (for training the subdomain networks), the error for approximating the initial condition (1b), and the error of Rankine-Hugoniot conditions (for training the networks dedicated to DLs).

The loss functional is nonlinear, and the associated minimization problem is not easy. In the machine learning community, these problems are typically solved with a gradient descent method, or variants of it. In this paper we use a global gradient method. We propose also a domain decomposition method (DDM) for the minimization problem, which allows the decoupling of the computation of the local solutions and DLs, hence allowing for an embarrassingly parallel computation, see [19, 20].

Notice that in this paper we focus on one-dimensional HCLs. We present a proof of concept, as well as some analytical arguments justifying the application or extension to high dimensional problems. In future works, we plan to apply the derived methodology to high dimensional problems.