Table of Links
Abstract, Acknowledgements, and Statements and Declarations
-
Background and Related Work
-
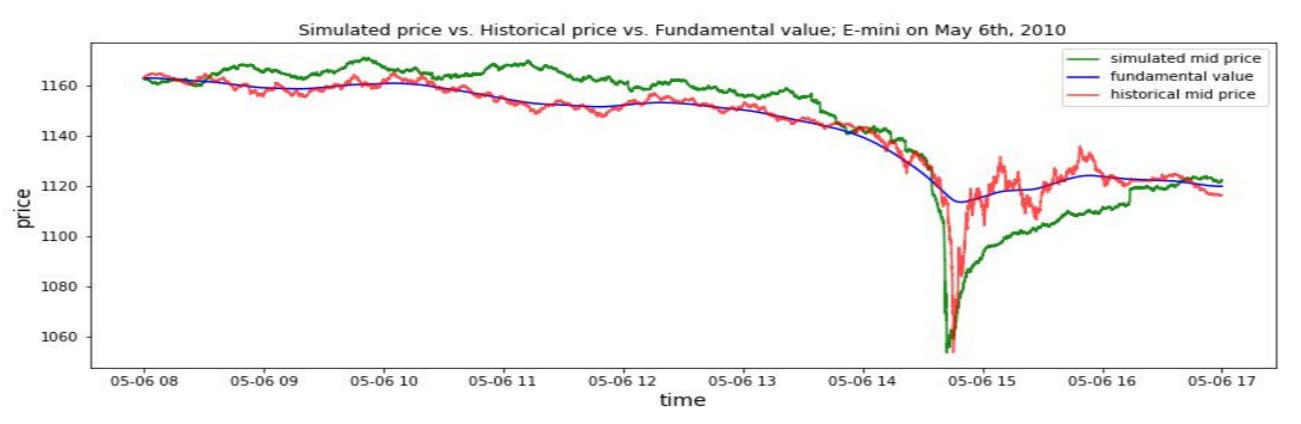
2010 Flash Crash Scenarios and 5.1 Simulating Historical Flash Crash
-
Mini Flash Crash Scenarios and 6.1 Introduction of Spiking Trader (ST)
-
Conclusion and Future Work
3 Model Structure
This section presents the set-up and components of the proposed agent-based high-frequency financial market simulator.
3.1 Model Set-up
3.2 Common Trader Behaviours
Traders in our simulation model have some behaviours in common, for example submitting and cancelling orders. We can assume that there is a certain type of agent called "Base Agent", and all traders in our model inherit the functionalities of this base agent. Specifically, all traders in the model have common behaviours as follows.
• Each trader has a parameter θ, which controls the probability of submitting a limit order. The value of θ depends on the type of traders and also varies during simulation, but the behaviour given a θ value is common for all types of traders. That is, for each simulation step, if p ∈ U(0, 1)[4] < θ, the trader will place an limit order, otherwise no action is taken. Note that the specific side of the order (buy or sell) depends on the trader type and market conditions. The value of θ could be zero for some traders, which means that the corresponding traders do not submit limit orders.
• Each trader has a parameter µ. The function of µ is identical to parameter θ, except that µ controls the probability of sending a market order. Similar to θ, the value of µ is different for different types of traders and varies for different timestamps. For each simulation step, if p ∈ U(0, 1) < µ, the trader will place a market order, otherwise no action is taken. The specific side of the market order also depends on the trader type and market conditions. Similar to θ, the value of µ can also be zero for some particular type of traders.
• Each type of trader has a parameter δ. Regardless of the order price and side, each limit order has a cancellation probability of δ at each simulation step. The value of δ is dependent on the type of trader who places the order, and is calibrated using historical market data to create realistic limit order book behaviours. In the presented model, all traders share the same value for δ except market makers, who have a higher value of δ. This reflects the fact that orders submitted by market makers tend to have a much higher cancellation / replacement rate.
• In the proposed model, short-term momentum traders, long-term momentum traders and noise traders all have a parameter called ρ, which controls the ratio between the number of market orders and limit orders placed by the same trader. That is, for each trader of these three types, there is a fixed relationship between θ and µ: µ = θ ∗ ρ. This relationship enables a realistic ratio between the number of market orders and limit orders in the simulated financial market and the value of ρ is selected according to historical orders data.
• The volume V for each order is 100, regardless of limit order or market order.
Despite the common trader behaviours, each type of trader follows different trading heuristics and has different values for the associated parameters. For example, fundamental traders only submit market orders. Market makers submit limit orders in normal trading time. Only after the inventory limit is hit will market makers submit market orders to reduce their inventory risk. The remaining types of traders submit both limit orders and market orders during trading hours, aiming to maintain a fixed ratio between the number of limit orders and the number of market orders. The remainder of the section describes the trading behaviour heuristics for each type of trader in more detail. Descriptions for all the parameters involved in the proposed model are summarised in Appendix A.
3.3 Fundamental Trader (FT)
Authors:
(1) Kang Gao, Department of Computing, Imperial College London, London SW7 2AZ, UK and Simudyne Limited, London EC3V 9DS, UK ([email protected]);
(2) Perukrishnen Vytelingum, Simudyne Limited, London EC3V 9DS, UK;
(3) Stephen Weston, Department of Computing, Imperial College London, London SW7 2AZ, UK;
(4) Wayne Luk, Department of Computing, Imperial College London, London SW7 2AZ, UK;
(5) Ce Guo, Department of Computing, Imperial College London, London SW7 2AZ, UK.
This paper is available on arxiv under CC BY-NC-ND 4.0 DEED license.