Authors:
(1) Sankarshan Damle, IIIT, Hyderabad, Hyderbad, India ([email protected]);
(2) Manisha Padala, IISc, Bangalore, Bangalore, India ([email protected]);
(3) Sujit Gujar, IIIT, Hyderabad, Hyderbad, India ([email protected]).
Table of Links
-
IDEAL-TFRM: Impossibility of Achieving Strictly Positive Redistribution Index
-
R-TFRM: A TFRM Robust to Miner Manipulation
6.1 R-TFRM: Analyzing Impact of Miner Manipulation on Rebate and Miner Revenue
A. Proofs for Results from Section 4 and 5
B. Proofs for Results from Section 6
C. Proofs for Results from Section 7
ABSTRACT
Blockchains deploy Transaction Fee Mechanisms (TFMs) to determine which user transactions to include in blocks and determine their payments (i.e., transaction fees). Increasing demand and scarce block resources have led to high user transaction fees. As these blockchains are a public resource, it may be preferable to reduce these transaction fees. To this end, we introduce Transaction Fee Redistribution Mechanisms (TFRMs) – redistributing VCG payments collected from such TFM as rebates to minimize transaction fees. Classic redistribution mechanisms (RMs) achieve this while ensuring Allocative Efficiency (AE) and User Incentive Compatibility (UIC). Our first result shows the non-triviality of applying RM in TFMs. More concretely, we prove that it is impossible to reduce transaction fees when (i) transactions that are not confirmed do not receive rebates and (ii) the miner can strategically manipulate the mechanism. Driven by this, we propose Robust TFRM (R-TFRM): a mechanism that compromises on an honest miner’s individual rationality to guarantee strictly positive rebates to the users. We then introduce robust and rational TFRM (R 2 -TFRM) that uses trusted on-chain randomness that additionally guarantees miner’s individual rationality (in expectation) and strictly positive rebates. Our results show that TFRMs provide a promising new direction for reducing transaction fees in public blockchains.
1 INTRODUCTION
Public blockchains have achieved mainstream prominence with Bitcoin [29] and Ethereum [4] processing > 1𝑀 transactions daily [38, 39]. Most commonly, public blockchains comprise a cryptographically linked series of blocks. Each block may consist of several individual transactions. Miners, tasked with block creation, add a subset of transactions from the set of outstanding transactions (referred to as mempool). To incentivize miners to add their transaction to the block, transaction creators (henceforth users) include a fee as a commission. The fee absorbs the users’ valuation for their transaction being added to the block. Roughgarden [33] proposes transaction fee mechanisms (TFMs) to study the strategic interaction between the miner and the users.
Transaction Fee Mechanism (TFM). TFMs resemble a classic auction setting. Users place a bid to include their transactions in the block, and the miner mimics an auctioneer to select the subset, which maximizes its revenue. E.g., Bitcoin’s TFM resembles a first-price auction, where the block’s miner greedily adds the transactions with the highest bids. Unfortunately, an increasing demand, cryptocurrency’s market volatility, and supply-demand economics have led to users’ over-paying [2]. E.g., Messias et al. [26] show that 30% of Bitcoin fees are two orders of magnitude more than recommended.
Considering public blockchains as a shared resource, it’s desirable not to impose charges for transaction confirmation. However, given the infeasibility of confirming every transaction due to resource constraints, one may prefer only to confirm transactions with higher value (pertaining to their importance to users). The absence of transaction fees could lead users to misrepresent the value of their transactions in order to secure confirmation. Therefore, this paper aims to design TFMs that minimize transaction fees while upholding other incentive-related properties.
Clearly, the minimization of transaction fees is at odds with the miner’s objective of maximizing revenue. Thus, the task of designing TFMs to minimize fees is more intricate than in the classical auction setting, primarily because, in TFMs, miners have complete control over the transactions they include in their blocks [33].
Our Goal. We aim to design a TFM that satisfies certain game theoretic properties like (i) Allocative Efficiency (AE): confirmed transactions maximize the overall valuation, (ii) User Incentive Compatibility (UIC): users bid their true valuation, and Individual Rationality (IR): users receive non-negative payoff. At the same time, the TFM must actively reduce transaction fees for users, thereby enhancing the blockchain’s appeal. Unfortunately, from the famous Green-Laffont Impossibility Theorem [25], we know that it is impossible to design a TFM that is both AE and UIC and which guarantees zero net transaction fees – in mechanism design commonly referred to as strong budget balance.
Given this, our objective is to design a TFM that is both AE and UIC while minimizing the transaction fees (or is weakly budget balanced). Motivated from Maskin et al. [25], the mechanism design literature proposes the use of Groves’ Redistribution Mechanism (RM) for this purpose [7, 17, 25]. In Groves’ RM, the VCG mechanism is executed, and then the surplus money is redistributed among the users while preserving other game-theoretic properties.
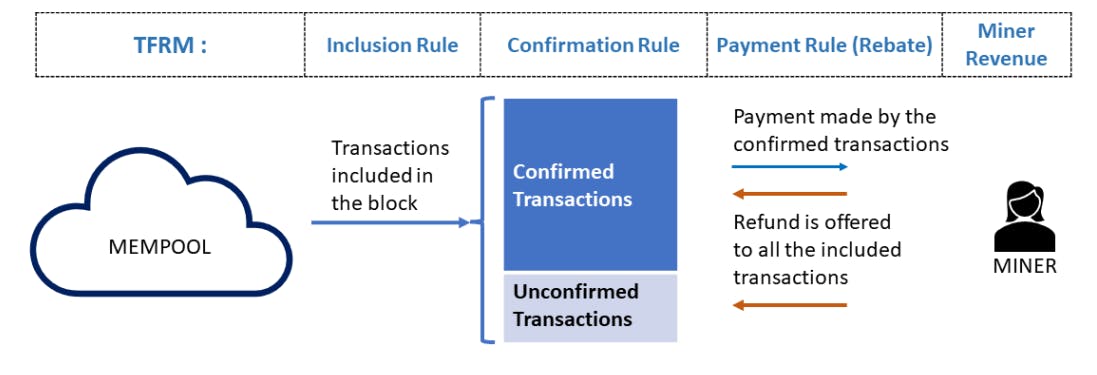
Along similar lines, this paper introduces Transaction Fee Redistribution Mechanisms (TFRMs): a general class of TFMs based on RMs where the miner offers rebates from the transaction fees collected to the users while retaining AE, UIC, and IR. By offering users rebates, TFRMs, in effect, reduce the transaction fees paid by them. Figure 1 provides an overview.
TFRM: Challenges. Designing such TFRMs has the following primary challenges.
Miner IC (MIC): As miners possess complete control over the transactions included in their blocks [33], they may deviate from the
intended TFM allocation rule (i.e., selecting a different subset from the mempool) and may introduce “fake” transactions (i.e., transactions created strategically to increase their revenue) into their blocks [33]. This is similar to shill bidding [32] in traditional auctions. Thus, it is imperative that a TFRM maintains AE, UIC, and low transaction fees even in the face of miner manipulation (or, alternately, in the presence of a strategic miner).
Roughgarden [33] introduces the notion of miner IC (MIC) to model the miner’s strategic behavior. In auction theory, the MyersonSatterthwaite impossibility theorem [28] states that it is impossible to design a mechanism that is AE, IR, weakly budget balanced, and IC for both sides of the market. Designing TFRMs is analogous to such a two-sided auction, and achieving both sides’ IC (with other properties) is elusive.
User IC (UIC): Typically, RMs ensure UIC by offering rebates to everyone participating in the auction (irrespective of the allocation). In TFRMs, the transactions that are only part of the mempool (i.e., are not part of the block) are not available to the blockchain. Thus, unlike RMs, in TFRMs, we cannot offer rebates for each available transaction. As some transactions do not receive rebates, we can easily construct instances where the users of these transactions have an incentive to overbid to get included in the block and receive rebates. Thus, ensuring UIC in TFRM is non-trivial. As such, we propose restricted UIC (RUIC), which ensures that bidding truthfully is a weakly dominant strategy only for the users whose transactions are included in the block.
Our Contributions. Broadly, we (i) formally introduce TFRMs (refer to Figure 1 for an overview), (ii) analyze the challenges due to miner manipulation in vanilla-TFRMs, and (iii) introduce two novel TFRMs, namely R-TFRM and R 2 -TFRM that are robust to miner manipulation. We discuss these in detail next.
(1) Ideal-TFRM. As we cannot offer rebates to all transactions in the mempool, we begin our analysis with an “Ideal-TFRM" that offers non-zero rebates only to confirmed transactions. Unfortunately, we show that it is impossible for Ideal-TFRM to satisfy UIC while offering non-zero rebates to confirmed transactions (Theorem 2).
(2) TFRM: Effect of A Strategic Miner. We shift our focus to TFRMs that provide rebates to all transactions included in the block. An RM’s effectiveness is measured using the Redistribution Index (RI) [18], which is the fraction of the VCG surplus redistributed. To absorb the effect of strategic miners, we introduce Resilient Redistribution Index (RRI). RRI measures the fraction of redistributed funds under optimal miner manipulation. We prove that it is impossible to design a TFRM that satisfies AE, RUIC, and is IR for both users (IR𝑢) and miners (IRM), while guaranteeing strictly positive RRI (Theorem 3).
(3) Robust TFRM (R-TFRM). Given these impossibilities, we propose R-TFRM: a TFRM that guarantees strictly positive RRI and satisfies all user-specific properties. However, R-TFRM is not individually rational for the miner[1].
At its core, R-TFRM builds on an RM with VCG payments as transaction fees and a linear rebate function. The rebate function maximizes the worst-case rebate while satisfying RUIC, IR𝑢, and Approx-IRM. Designing such a rebate function is equivalent to solving the linear program in Figure 4 for its coefficients. We finally show that the payments are reduced by a fraction 𝑘/𝑛, where 𝑘 transactions are confirmed out of the 𝑛 included in the block (Theorem 5). The fraction remains the same, even with miner manipulation, i.e., RRI is also 𝑘/𝑛. In other words, each confirmed user sees a reduction by (1 − 𝑘/𝑛) in its transaction fee compared to the equivalent VCG-based TFM.
This paper is
[1] We remark that miners, or block proposers in general, often have alternate revenue streams (e.g., block rewards [29] or attestation rewards [35]). These rewards can primarily help absorb the reduction in revenue due to reduced transaction fees. They may also alleviate the lack of IRM guarantee in R-TFRM.