Does LoRA Fine-Tuning Help AI Models Forget Less?

Table of Links

Abstract and 1 Introduction

2 Background

3 Experimental Setup and 3.1 Datasets for Continued Pretraining (CPT) and Instruction Finetuning (IFT)

3.2 Measuring Learning with Coding and Math Benchmarks (target domain evaluation)

3.3 Forgetting Metrics (source domain evaluation)

4 Results

4.1 LoRA underperforms full finetuning in programming and math tasks

4.2 LoRA forgets less than full finetuning

4.3 The Learning-Forgetting Tradeoff

4.4 LoRA’s regularization properties

4.5 Full finetuning on code and math does not learn low-rank perturbations

4.6 Practical takeaways for optimally configuring LoRA

5 Related Work

6 Discussion

7 Conclusion and References

Appendix

A. Experimental Setup

B. Learning rate searches

C. Training Datasets

D. Theoretical Memory Efficiency Gains with LoRA for Single and Multi-GPU Settings

4.3 The Learning-Forgetting Tradeoff

It is trivial that models that change less when finetuned to a new target domain, will forget less of the source domain. The nontrivial question is: do LoRA and full finetuning differ in how they tradeoff learning and forgetting? Can LoRA achieve similar target domain performance but with diminished forgetting?

We form a learning-forgetting Pareto curve by plotting the aggregate forgetting metric vs. the learning metric (GSM8K and HumanEval), with different models (trained for different durations) scattered as points in this space (Fig. 4). LoRA and full finetuning seem to occupy the same Pareto curve, with the LoRA models on the lower right – learning less and forgetting less. However, we are able find cases, especially for code IFT, where for a comparable level of target-domain performance, LoRA exhibits higher source-domain performance, presenting a better tradeoff. In supplementary Fig. S5 we show the raw evaluation scores for each model. In Fig. S3 we scatter the Llama-2-13B results in the same plot as Llama-2-7B for Code CPT.

4.4 LoRA’s regularization properties

Here, we define regularization (loosely) as a training mechanism that keeps the finetuned LLM similar to the base LLM. We first analyze similarity in the learning-forgetting tradeoff and then in the generated text.

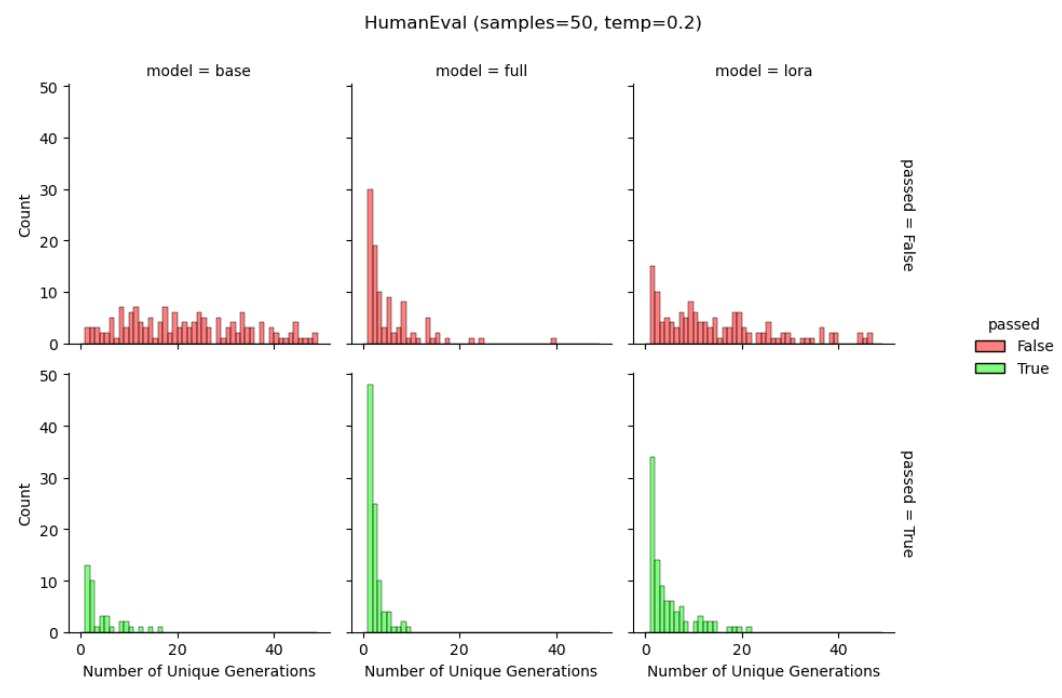
LoRA helps maintain diversity of token generations. We again use Llama-2-7B models trained on Magicoder-Evol-Instruct-110K dataset to scrutinize the generated strings during HumanEval. We calculate the unique number of output strings out of 50 generations (for base model, full finetuning, and LoRA) serving as a coarse proxy for predictive diversity. In Figure 6 we separately show the results for correct and incorrect answers. As in the reinforcement learning from human feedback literature (Du et al., 2024; Sun et al., 2023), we find that full finetuning results in fewer unique generations (“distribution collapse”) compared to the base model, for both pass and fail generations. We find that LoRA provides a compromise between the two, at the

level of generations. The above works also suggest that LoRA could even substitute a common regularization term that keeps the probabilities of the generated text similar between the finetuned and base model.