Dear readers & friends,
Studies have shown over and over that even professional researchers (including statisticians!) can’t correctly interpret a confidence interval or a p-value most of the time. Then, how could you expect the average Joe to be better at that? Frequentist statistics (the kind that gives you those confidence intervals and p-values) just isn’t meant to be intuitive. I’ve written before about how this—and especially a blind reliance on “statistical significance”—can lead businesses down the wrong path.
Interestingly, what many people in industry intuitively believe are conclusions you can draw from frequentist analyses—like, “there’s an X% chance of Y% uplift” or “there’s a 95% chance the true uplift lies between X% and Y%”—are statements you could actually conclude … if you had used Bayesian statistics. Many tools and platforms (e.g., for online experimentation) have started integrating Bayesian approaches, but practitioners still need to become more familiar with them, because frequentist analyses are still the predominant, “traditional” way of doing statistics in industry.
Now, what’s one of the best ways to get started with Bayesian statistics? Obviously, creating your own Bayesian A/B testing tool from scratch. And that’s exactly what we’re doing in my latest article in The UX Collective, “Bayesian A/B testing—a practical primer* (for UX people and anyone who wants to experiment better; some willingness to deal with statistics and Python required).”
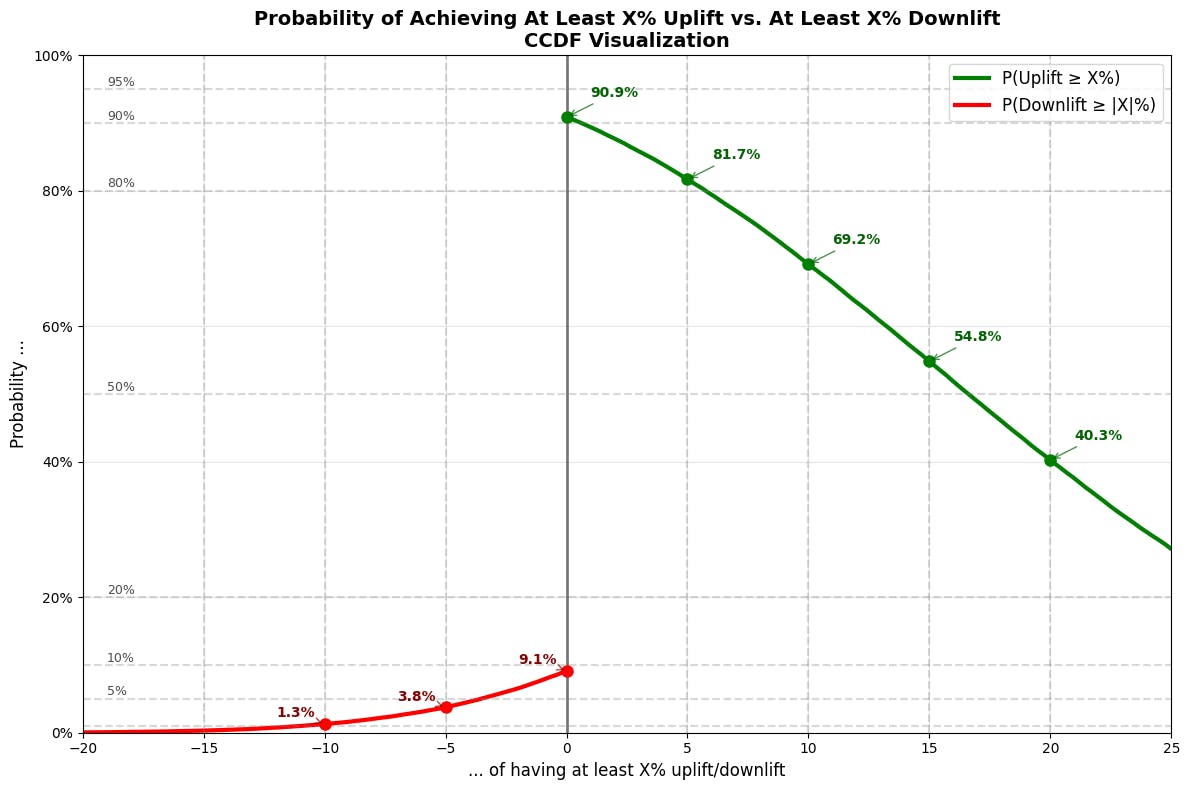
Step by step, the article takes you through the entire process, starting with just the numbers of visitors and conversions in two variations of an A/B test and ultimately arriving at a complementary cumulative distribution function (see below) giving you the entire range of probabilities for all possible uplifts. It’s not at all as complicated as it might sound—I promise! (But you might want to read up a bit on basic statistics and programming in Python, if necessary).
Why this matters for UX practitioners
The beauty of Bayesian thinking extends far beyond A/B testing. It mirrors how we naturally think about uncertainty in design decisions. When you're weighing whether to implement a new feature, you shouldn’t be looking for a binary yes/no answer—you should considering probabilities, trade-offs, and the range of possible outcomes.
Traditional frequentist approaches (while not being worse—or better—than Bayesian!) can force UX people into artificial certainty thresholds that don’t reflect the messy reality of product development. Bayesian methods give us permission to embrace uncertainty while still making data-informed decisions.
Reading recommendations
Since we’re diving deep into statistical thinking, here are some resources that complement the rather technical article:
📖 Thinking, Fast and Slow by Daniel Kahneman remains essential reading for understanding how our brains naturally (mis)handle probability and uncertainty—and in general one of the most important books for any human to read.
📖 The Theory That Would Not Die by Sharon Bertsch McGrayne tells the fascinating history of Bayesian statistics and why it took so long to gain acceptance, despite being more intuitive than frequentist approaches.
Tool recommendations
🛠️ If you’re not ready to dive into Python just yet, Dynamic Yield's Bayesian A/B Testing Calculator is a free web-based tool that lets you input your test data and immediately see Bayesian probability calculations without any subscription required. It’s perfect for experimenting around a bit.
🛠️ For those wanting to go deeper, PyMC is an excellent Python library for Bayesian modeling that goes well beyond A/B testing.
The goal isn’t to become a statistician overnight, but to develop a more nuanced relationship with uncertainty in our work. After all, UX itself is fundamentally about making decisions under uncertainty—we might as well get better at thinking about it.
As always, I’d love to hear your thoughts on this. Have you encountered situations where traditional statistical significance led your team astray? Or are you already experimenting with Bayesian approaches? Simply reply to share your experiences. 🙏🏻
Cheers,
Max
☕ I love coffee, and if you want to support my work, you can always