In many applications, generating a unique user identifier is a common task that is frequently taken for granted. A simple, effective way to generate user identifiers is to generate a large random number, and let the properties of small probabilities all but guarantee that each generated number will be different from any previously generated identifiers (see: UUIDv4, or cryptographic nonces).
Suppose that you don’t feeling like breaking out the pencil, paper, and brain to work out the collision probabilities as the size of your user base increases. Instead, you reach for a nearby, relatively crumb-free keyboard and decide to amuse yourself by writing a simulation.
The program is simple. It executes the following:
- Create a map / dict / object data structure to serve as an associative array.
- Set the global collision counter to 0.
- Generate a random 53-bit random integer (in order to allow parity with Javascript, which only allows 53-bit integers).
- Check if this number exists in the associative array. If it does not, add it to the array. If it does, increment the global collision counter.
- Jump to step 3 until the program crashes due to hitting a 2 GB memory limit.
This is clearly a simple program that can be written in multiple ways (for example, by using each language’s set data structure). However, the point of this micro-benchmark is to roughly answer the following questions for a number of languages:
- How many unique integers can we stuff into an associative array before the program crashes?
- How much time does each language take to get to its crash point?
And of course, to see how many collisions are actually encountered.
The contenders are as follows. Before looking at the results, try to formulate your guesses for the answers to the questions above for each language.
- C++ compiled with gcc 5.4.0 and C++11 support
- Python 2 running on CPython 2.7.12
- Python 2 running on PyPy 5.1.2
- Python 3 running on CPython 3.5.2
- node.js 6.11.3 (LTS as of September 2017)
- node.js 8.4.0 (latest as of September 2017)
Results
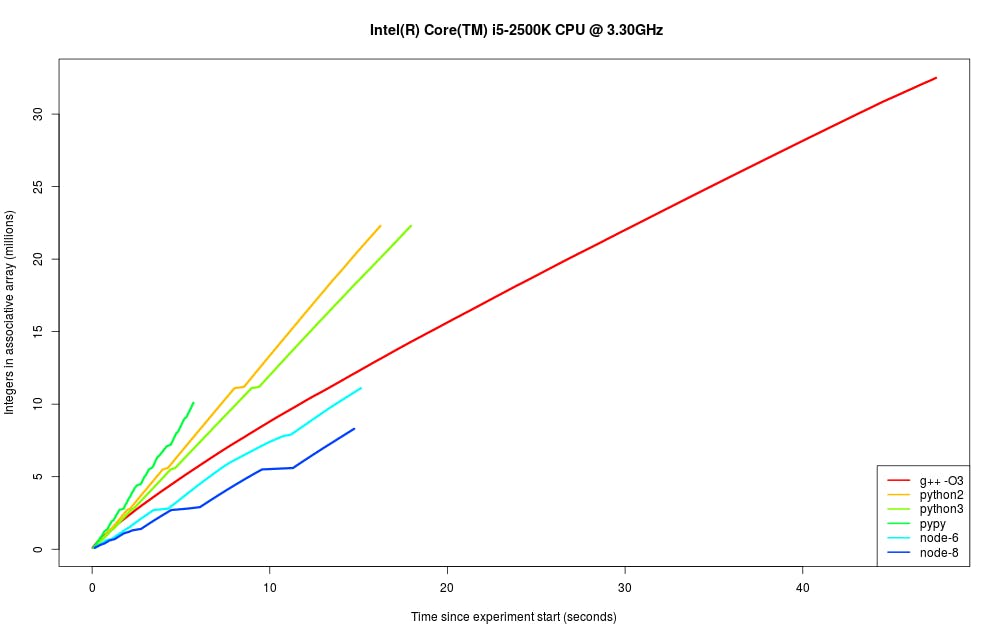
The graph below shows the number of unique integers put into the associative array before the program either hit the 2 GB memory limit, or crashed for other reasons.
The x-axis is time since the program was started, and the y-axis is the number of integers in the associative map in millions. In this graph, lines terminate when the program crashes. Steeper lines represent faster associative array performance, since a lookup and insertion is performed at each iteration of the loop.
- Naturally, C++ achieves the best memory performance, storing more than 32.5 million long integers in a std::map before crashing. However, Python exceeds its performance in terms of speed, as seen by the steeper lines for all three implementations. This may be somewhat unexpected to people accustomed to C/C++ being the gold standard for performance, but can be explained by the fact that Python uses a plain hash map as the implementation for its dict data structure, whereas C++’s map uses a red-black tree.
- Running CPython in Python 2 and 3 modes show very similar performance profiles, with Python 2 being a tad faster than Python 3 at storing the same number of items — about 22.3 million integers.
- Pypy’s performance exceeds that of CPython in both Python 2 and 3 flavors, but its memory management causes it to crash after adding just 10 million integers to the map.
- node.js shows the worst memory performance characteristics. Of these, the current LTS release of node (v6) is slightly better than the latest release (v8). However, both are not only the slowest profiled here, but also show among the worst memory performance. Node 6 stores just 11.1 million integers in an object, and node 8 fares the worst with 8.3 million integers.
As for the original intent of this expedition, the total number of collisions across all runs for all languages was precisely 0.
Code and raw results
Notes
- g++ was run with -O3 and with the C++11 standard.
- node 8.4.0 hung without crashing after consuming approximately 1.1 GB of memory. This is in spite of running with the — max-old-space-size=2048 command line flag. Without limiting process memory using ulimit, memory consumption appeared to increase without bound, in spite of producing no new output. Disabling TurboFan using — noturbo had no impact. Disabling garbage collection using — noconcurrent_sweeping also had no impact.
- node 6.11.3’s garbage collector prints its crash stack trace to stdout instead of stderr, which is non-standard behavior.