Table of Links
Abstract, Acknowledgements, and Statements and Declarations
-
Background and Related Work
-
2010 Flash Crash Scenarios and 5.1 Simulating Historical Flash Crash
-
Mini Flash Crash Scenarios and 6.1 Introduction of Spiking Trader (ST)
-
Conclusion and Future Work
5.2 Flash Crash Under Different Conditions
The above presents an analysis of the market dynamics during the simulated flash crash event. A natural question to follow is what factors contribute to the sharp price drop. One significant advantage of the agent-based model is the ability to be simulated multiple times under different conditions to reproduce realistic market events, while the historical event only happens once. This makes agent-based model a perfect testbed for exploring the conditions that lead to various rare market events, such as the flash crash. In this section, we explore the conditions that would influence the severity of flash crash events.
The main methodology applied here is Monte Carlo simulation experiments under controlled conditions. The conditions are represented by model parameters. Each combination of model parameters corresponds to a specific market condition configuration. For each combination of model parameters, multiple simulations are carried out. For each simulation, the amplitude of the simulated flash crash is calculated. In this way a distribution of flash crash amplitudes is obtained. To reduce the influence of extreme values, the 50% quantile of all the Monte Carlo simulated amplitudes is defined as the flash crash amplitude associated with the condition that is represented by the specific combination of model parameters. The 40% and 60% quantile of the simulated flash crash amplitudes are also recorded.
Percentage of Volume for the Sell Algorithm
One important parameter that characterises the Sell Algorithm is the percentage of volume r, which determines the target execution rate of the Sell Algorithm. Specifically, r is the percentage of the market trading volume calculated over the previous minute that the Sell Algorithm aims to execute. Monte Carlo simulation is carried out with different values for r, while other model parameters are given the previous calibrated values and are strictly kept constant. Panel (a) in Figure 9 shows the relationship between the simulated flash crash amplitude and the percentage of volume r.
It is shown that when r is small, the amplitude of the flash crash is limited. When r is increased, the flash crash amplitude is also enlarged. Within a certain range, the more aggressive the Sell Algorithm (larger r), the more severe the flash crash event (larger amplitude). This phenomenon is consistent with our intuition. One interesting phenomenon is that after r exceeds 5%, the flash crash amplitude barely changes even though we continue to increase the value of r. The reason is that as long as the price reaches a certain lower level, the demand generated from fundamental traders is large enough to digest the inventory of the institutional trader. Since the total inventory of the institutional trader is fixed, the lowest price that could be reached during the simulation barely changed. Consequently, the flash crash amplitude stops increasing despite larger values for r.
The lessons learned from this experiment mainly involves the choice of the algorithmic trading strategies for large institutional traders. The market impact of an algorithmic trading strategy may contradict our intuition, as is the case here when r is larger than 5%. Instead, the complex interaction between an algorithmic trading strategy and other market participants is likely to cause unexpected consequences. It is strongly recommended that institutional traders deploy agent-based financial market simulation to explore potential consequences before choosing a specific algorithmic trading strategy.
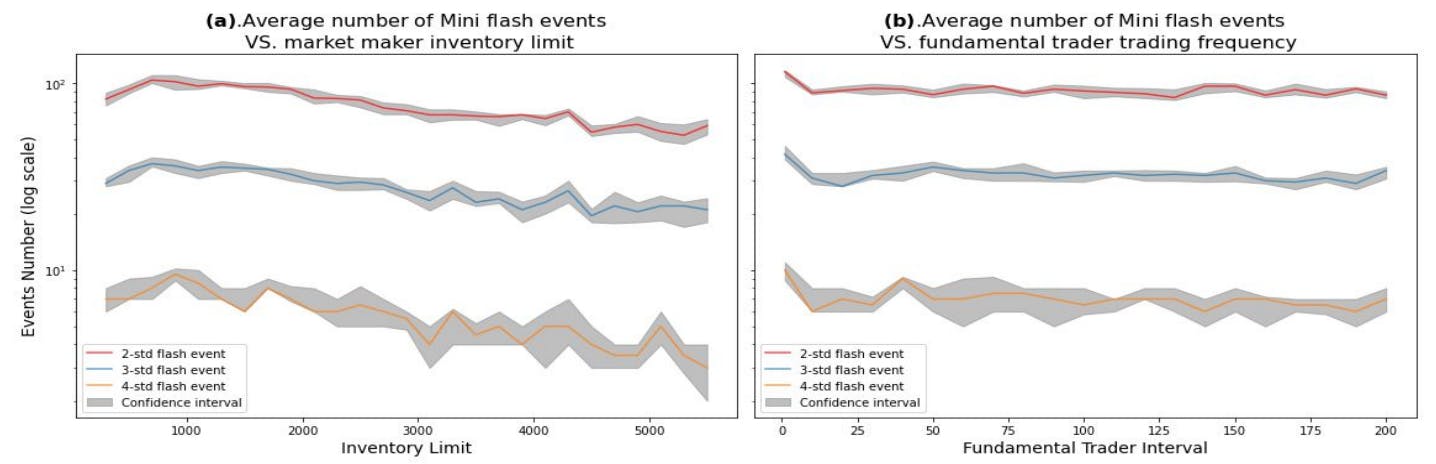
Inventory limit for market makers
The analysis here emphasizes the importance of risk management for high-frequency market makers. Since all market makers have some sort of inventory control, the decreasing part of panel (b) in Figure 9 is hardly feasible in the real-world trading environment. Instead, most real-world market makers have inventory limits that lie on the increasing part of the curve. An individual market maker may consider his own inventory limit to be proper; however, multiple "proper" inventory limits combined may lead to a significant crash under stressed scenarios due to the "hot-potato" effect. In order to foster a smooth and stable market, experimental results suggest that policymakers could impose certain inventory limits on all high-frequency market makers.
Trading frequency for fundamental traders
The figure indicates that there is a monotonous relationship between flash crash amplitude and the trading frequency of fundamental traders. Note that the larger the interval is, the lower the trading frequency is. Thus the flash crash amplitude is decreasing when we increase the trading frequency of fundamental traders. If the fundamental traders have the same trading frequency as the market makers, the flash crash amplitude becomes small enough that the flash crash turns into a small shock in the market.
The analysis here supports the argument that the mismatch of trading frequency between different types of traders potentially leads to flash crash events. There is hardly an imaginary "high-frequency fundamental trader" in the real-world trading environment. Thus practical trading environment corresponds to the right-hand part of the functional relationship in Panel (c) of Figure 9, where fundamental traders act at a lower frequency. The results indirectly show that high-frequency trader is an important factor in the occurrence of flash crash scenarios.
Authors:
(1) Kang Gao, Department of Computing, Imperial College London, London SW7 2AZ, UK and Simudyne Limited, London EC3V 9DS, UK ([email protected]);
(2) Perukrishnen Vytelingum, Simudyne Limited, London EC3V 9DS, UK;
(3) Stephen Weston, Department of Computing, Imperial College London, London SW7 2AZ, UK;
(4) Wayne Luk, Department of Computing, Imperial College London, London SW7 2AZ, UK;
(5) Ce Guo, Department of Computing, Imperial College London, London SW7 2AZ, UK.
This paper is available on arxiv under CC BY-NC-ND 4.0 DEED license.