LoRA Learns Less and Forgets Less—Is that a Bug or a Feature?

Table of Links

Abstract and 1 Introduction

2 Background

3 Experimental Setup and 3.1 Datasets for Continued Pretraining (CPT) and Instruction Finetuning (IFT)

3.2 Measuring Learning with Coding and Math Benchmarks (target domain evaluation)

3.3 Forgetting Metrics (source domain evaluation)

4 Results

4.1 LoRA underperforms full finetuning in programming and math tasks

4.2 LoRA forgets less than full finetuning

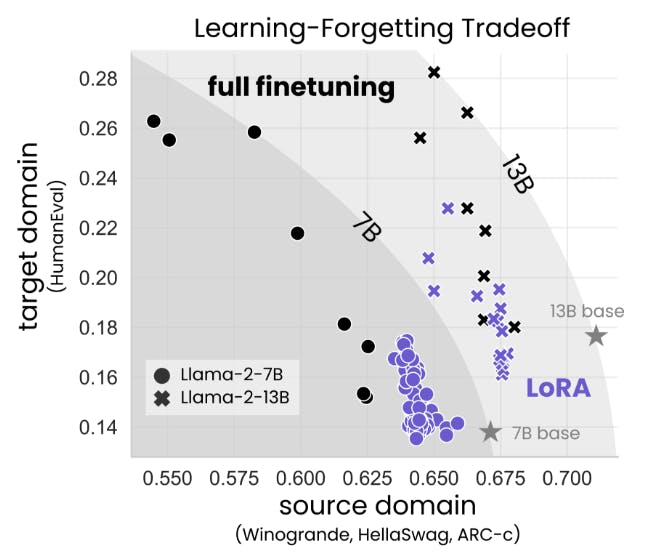
4.3 The Learning-Forgetting Tradeoff

4.4 LoRA’s regularization properties

4.5 Full finetuning on code and math does not learn low-rank perturbations

4.6 Practical takeaways for optimally configuring LoRA

5 Related Work

6 Discussion

7 Conclusion and References

Appendix

A. Experimental Setup

B. Learning rate searches

C. Training Datasets

D. Theoretical Memory Efficiency Gains with LoRA for Single and Multi-GPU Settings

Abstract

Low-Rank Adaptation (LoRA) is a widely-used parameter-efficient finetuning method for large language models. LoRA saves memory by training only low rank perturbations to selected weight matrices. In this work, we compare the performance of LoRA and full finetuning on two target domains, programming and mathematics. We consider both the instruction finetuning (≈100K prompt-response pairs) and continued pretraining (≈10B unstructured tokens) data regimes. Our results show that, in most settings, LoRA substantially underperforms full finetuning. Nevertheless, LoRA exhibits a desirable form of regularization: it better maintains the base model’s performance on tasks outside the target domain. We show that LoRA provides stronger regularization compared to common techniques such as weight decay and dropout; it also helps maintain more diverse generations. We show that full finetuning learns perturbations with a rank that is 10-100X greater than typical LoRA configurations, possibly explaining some of the reported gaps. We conclude by proposing best practices for finetuning with LoRA.

1 Introduction

Finetuning large language models (LLMs) with billions of weights requires a non-trivial amount of GPU memory. Parameter-efficient finetuning methods reduce the memory footprint during training by freezing a pretrained LLM and only training a small number of additional parameters, often called adapters. Low-Rank Adaptation (LoRA; Hu et al. (2021)) trains adapters that are low-rank perturbations to selected weight matrices.

Since its introduction, LoRA has been touted as a strict efficiency improvement that does not compromise accuracy on the new, target domain (Hu et al., 2021; Dettmers et al., 2024; Raschka, 2023; Zhao et al., 2024b). However, only a handful of studies benchmark LoRA against full finetuning for LLMs with billions of parameters, (Ivison et al., 2023; Zhuo et al., 2024; Dettmers et al., 2024), reporting mixed results. Some of these studies rely on older models (e.g. RoBERTa), or coarse evaluation benchmarks (such as GLUE or ROUGE) that are less relevant for contemporary LLMs. In contrast, more sensitive domain-specific evaluations, e.g., code, reveal cases where LoRA is inferior to full finetuning (Ivison et al., 2023; Zhuo et al., 2024). Here we ask: under which conditions does LoRA approximate full finetuning accuracy on challenging target domains, such as code and math?

By training fewer parameters, LoRA is assumed to provide a form of regularization that constrains the finetuned model’s behavior to remain close to that of the base model (Sun et al., 2023; Du et al., 2024). We also ask: does LoRA act as a regularizer that mitigates “forgetting” of the source domain?

In this study, we rigorously compare LoRA and full finetuning for Llama-2 7B (and in some cases, 13B) models across two challenging target domains, code and mathematics. Within each domain, we explore two training regimes. The first is instruction finetuning, the common scenario for LoRA involving question-answer datasets with tens to hundreds of millions of tokens. Here, we use Magicoder-Evol-Instruct-110K (Wei et al., 2023) and MetaMathQA (Yu et al., 2023). The second regime is continued pretraining, a less common application for LoRA which involves training on billions of unlabeled tokens; here we use the StarCoder-Python (Li et al., 2023) and OpenWebMath (Paster et al., 2023) datasets (Table 1).

We evaluate target-domain performance (henceforth, learning) via challenging coding and math benchmarks (HumanEval; Chen et al. (2021), and GSM8K; Cobbe et al. (2021)). We evaluate source-domain forgetting performance on language understanding, world knowledge, and common-sense reasoning tasks (Zellers et al., 2019; Sakaguchi et al., 2019; Clark et al., 2018).

We find that for code, LoRA substantially underperforms full finetuning, whereas for math, LoRA closes more of the gap (Sec. 4.1), while requiring longer training. Despite this performance gap, we show that LoRA better maintains source-domain performance compared to full finetuning (Sec. 4.2). Furthermore, we characterize the tradeoff between performance on the target versus source domain (learning versus forgetting). For a given model size and dataset, we find that LoRA and full finetuning form a similar learning-forgetting tradeoff curve: LoRA’s that learn more generally forget as much as full finetuning, though we find cases (for code) where LoRA can learn comparably but forgets less (Sec. 4.3).

We then show that LoRA – even with a less restrictive rank – provides stronger regularization when compared to classic regularization methods such as dropout (Srivastava et al., 2014), and weight decay (Goodfellow et al., 2016). We also show that LoRA provides regularization at the output level: we analyze the generated solutions to HumanEval problems and find that while full finetuning collapses to a limited set of solutions, LoRA maintains a diversity of solutions more similar to the base model (Sun et al., 2023; Du et al., 2024).

Why does LoRA underperform full finetuning? LoRA was originally motivated in part by the hypothesis that finetuning results in low-rank perturbations to the base model’s weight matrix (Li et al., 2018; Aghajanyan et al., 2020; Hu et al., 2021). However, the tasks explored by these works are relatively easy for modern LLMs, and certainly easier than the coding and math domains studied here. Thus, we perform a singular value decomposition to show that full finetuning barely changes the spectrum of the base model’s weight matrices, and yet the difference between the two (i.e. the perturbation) is high rank. The rank of the perturbation grows as training progresses, with ranks 10-100× higher than typical LoRA configurations (Figure 7).

We conclude by proposing best practices for training models with LoRA. We find that LoRA is especially sensitive to learning rates, and that the performance is affected mostly by the choice of target modules and to a smaller extent by rank.

To summarize, we contribute the following results:

• Full finetuning is more accurate and sample-efficient than LoRA in code and math (Sec.4.1).

• LoRA forgets less of the source domain, providing a form of regularization (Sec. 4.2 and 4.3).

• LoRA’s regularization is stronger compared to common regularization techniques; it also helps maintaining the diversity of generations (Sec. 4.4).

• Full finetuning finds high rank weight perturbations (Sec. 4.5).

• Compared to full finetuning, LoRA is more sensitive to hyperparameters, namely learning rate, target modules, and rank (in decreasing order; Sec. 4.6).

2 Background