MetaMathQA: AI-Augmented Math Dataset with 395K Samples

Table of Links

Abstract and 1 Introduction

2 Background

3 Experimental Setup and 3.1 Datasets for Continued Pretraining (CPT) and Instruction Finetuning (IFT)

3.2 Measuring Learning with Coding and Math Benchmarks (target domain evaluation)

3.3 Forgetting Metrics (source domain evaluation)

4 Results

4.1 LoRA underperforms full finetuning in programming and math tasks

4.2 LoRA forgets less than full finetuning

4.3 The Learning-Forgetting Tradeoff

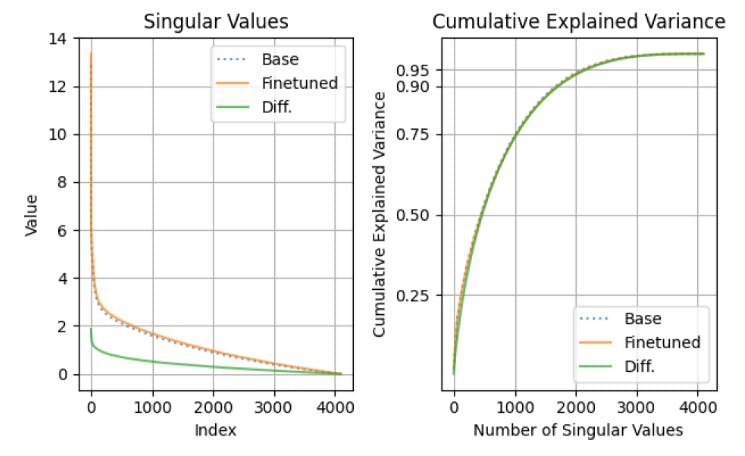
4.4 LoRA’s regularization properties

4.5 Full finetuning on code and math does not learn low-rank perturbations

4.6 Practical takeaways for optimally configuring LoRA

5 Related Work

6 Discussion

7 Conclusion and References

Appendix

A. Experimental Setup

B. Learning rate searches

C. Training Datasets

D. Theoretical Memory Efficiency Gains with LoRA for Single and Multi-GPU Settings

C Training Datasets

C.1 MetaMathQA (Math IFT)

The MetaMathQA dataset (Yu et al. (2023), https://huggingface.co/datasets/meta-math/MetaMathQA) contains 395,000 samples that are bootsrapped from the GSM (Cobbe et al., 2021) and Math (Hendrycks et al., 2021) training sets. These samples are augmented by GPT-3.5 using the following methods:

• Answer Augmentation (155k samples, Yu et al. (2023)): this method proposed by the MetaMathQA authors generates multiple reasoning paths for a given mathetical question and filters for generated reasoning paths that contain the correct final answer.

• Rephrasing (130k samples, (Yu et al., 2023)): this method proposed by the MetaMathQA authors uses GPT-3.5 to rephrase questions. They check for the correctness of rephrased questions by using few-shot Chain of Thought prompting to compare reasoning chains and proposed answers with ground truth answers.

Both Self-Verification (Weng et al., 2022) and FOBAR (Jiang et al., 2024) fall under the category of “backward reasoning,” where the question starts with a given condition and requires reasoning backwards to solve for an unknown variable. In order to generate new mathematical questions, a numerical value in the original question is masked as a variable X, and the question is rephrased accordingly.

MetaMathQA samples are organized by 4 columns: type, original_question, query and response.

We include two full examples below:

C.2 Magicoder-Evol-Instruct-110k (Code IFT)

C.3 Starcoder Python (Code CPT)

C.4 OpenWebMath (Math CPT)