Modeling Selfish Mining with Markov Decision Processes

Table of Links

Abstract and 1. Introduction

1.1 Related Work

2. Preliminaries

   2.1 System Model

   2.2 Selfish Mining Objective

   2.3 Markov Decision Processes

3. Selfish Mining Attack

   3.1 Overview

   3.2 Formal Model

   3.3 Formal Analysis

   3.4 Key Features and Limitations

4. Experimental Evaluation

5. Conclusion, Acknowledgments, and References

A. NAS Mining Objectives

B. Efficient Proof Systems

C. Proof of Theorem 3.1

3 SELFISH MINING ATTACK

3.1 Overview

Motivation. In order to motivate our selfish mining attack, we first recall the classic selfish mining attack strategy in Bitcoin [11]. Recall, the goal of the selfish mining strategy is to mine a private chain that overtakes the public chain (see Figure 1a). Selfish miners secretly fork the main chain and mine privately, adding blocks to a private, unannounced chain. These blocks are only revealed when the length of the private chain catches up with that of the main chain, forcing the honest miners to switch from the main to the private chain and waste computational resources. While in PoW blockchains each party mines on one block, in blockchains based on efficient proof systems parties can mine on multiple blocks due to ease of generating proofs. Our selfish mining attack exploits this observation by creating multiple private forks concurrently.

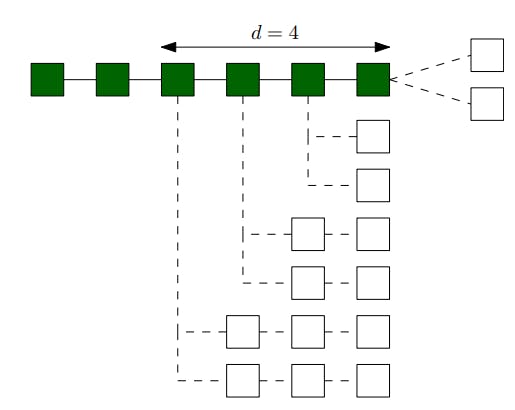
Outline of the attack. Our selfish mining attack proceeds with the adversary creating several private forks at different blocks in the main chain, see Figure 1b for an illustration. Rather than forking on the most recent block alone, the adversary creates up to 𝑓 forks on each of the last 𝑑 blocks on the main chain. Here, 𝑓 and 𝑑 are parameters of the attack where 𝑓 is the number of forks created at each public block and 𝑑 represents the depth of the adversary’s attack on the chain. One can view 𝑑 as the persistence parameter of the blockchain, which represents the depth at which earlier blocks are practically guaranteed to remain in the main chain [16]. At each time step, the adversary can either perform a

(1) mining action, i.e. attempt to mine a new block, or

(2) fork reveal action, i.e. publicly announce one of the private forks whose length is greater than or equal to that of the main chain.

Deciding on the optimal order of mining and fork reveal actions that the adversary should perform at each time step towards maximizing its expected relative revenue is a highly challenging problem. This is because, at each time step, the party to mine the next block is chosen probabilistically (see our System Model in Section 2.2), and the process results in a system with an extremely large number of states. For any given precision parameter 𝜖 > 0, our analysis will provide both an 𝜖-optimal strategy among selfish mining strategies that the adversary can follow, together with the exact value of the expected relative revenue guaranteed by this strategy.

Formal model of the attack. The goal of our analysis is to find an optimal selfish mining strategy which maximizes the expected relative revenue of the adversary. Note that this is a sequential decision making problem, since the optimal strategy under the above selfish mining setting must at every decision step optimally choose whether to perform a mining or a fork release action. Hence, in order to analyze this problem, in Section 3.2 we formally model our problem as an MDP. The state space of the MDP consists of all possible configurations of the main chain and private forks with the initial state corresponding to the time step at which the selfish mining attack is initiated. The action space of the MDP consists of the mining action as well as one fork release action for each private fork whose length is greater than or equal to that of the main chain. Finally, the probabilistic transition function of the MDP captures

the probabilistic process that generates and determines ownership (honest or adversarial) of new blocks to be added to the blockchain, as well as the process of determining the new main chain whenever the adversary publishes one or more private forks of equal length.

Formal analysis of the attack. Recall, the objective of our selfish mining attack is to maximize the expected relative revenue of the adversary. To do this, in Section 3.3 we define a class of reward functions in the MDP constructed in Section 3.2. We show that, for any 𝜖 > 0, we can compute an 𝜖-optimal selfish mining strategy in the MDP and the exact value of the expected relative revenue that it guarantees by solving the mean-payoff MDP with respect to a reward function belonging to the class of constructed reward functions. We solve mean-payoff MDPs by using off-the-shelf tools as mentioned in Section 2.3. Our analysis yields a fully automated method for computing 𝜖-optimal strategies and values of the expected relative revenue that provides formal guarantees on the correctness of its results.