Table of Links
-
Harnessing Block-Based PC Parallelization
4.1. Fully Connected Sum Layers
4.2. Generalizing To Practical Sum Layers
-
Conclusion, Acknowledgements, Impact Statement, and References
B. Additional Technical Details
6. Experiments
We evaluate the impact of using PyJuice to train PC models. In Section 6.1, we compare PyJuice against existing implementations regarding time and memory efficiency. To demonstrate its generality and flexibility, we evaluate PyJuice on four commonly used dense PC structures as well as highly unstructured and sparse PCs. Next, we demonstrate that PyJuice can be readily used to scale up PCs for various downstream applications in Section 6.2. Finally, in Section 6.3, we benchmark existing PCs on high-resolution image datasets, hoping to incentivize future research to develop better PC structures as well as learning algorithms.
5. Optimizing Backpropagation with PC Flows
While similar results have been established in a slightly different context (Peharz et al., 2020a), we prove the following equations in Appendix B.2 for completeness:
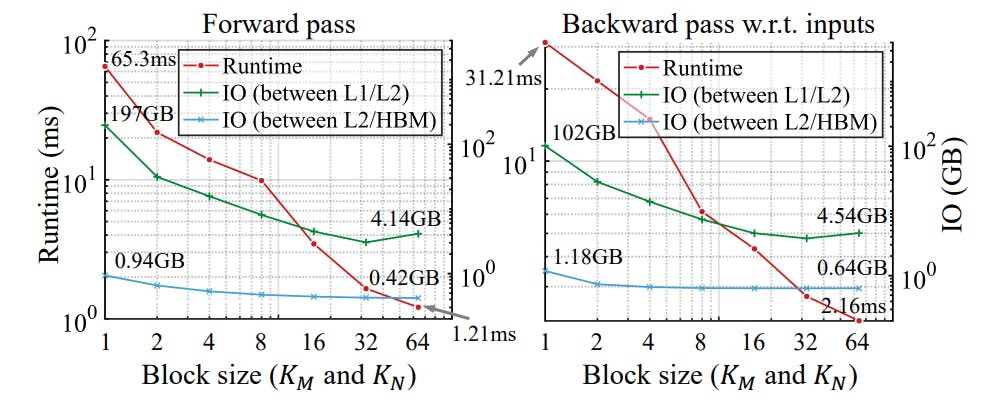
Another important design choice that leads to a significant reduction in memory footprint is to recompute the product nodes’ probabilities in the backward pass instead of storing them all in the GPU memory during the forward pass. Specifically, we maintain a scratch space on GPU HBM that 5 If such nodes exist, we can always collapse them into a single sum or product node. can hold the results of the largest product layer. All product layers write their outputs to this same scratch space, and the required product node probabilities are re-computed when requested by a sum layer during backpropagation. Since product layers are extremely fast to evaluate compared to the sum layers (e.g., see the runtime breakdown in Fig. 2), this leads to significant memory savings at the cost of slightly increased computation time.
Authors:
(1) Anji Liu, Department of Computer Science, University of California, Los Angeles, USA ([email protected]);
(2) Kareem Ahmed, Department of Computer Science, University of California, Los Angeles, USA;
(3) Guy Van den Broeck, Department of Computer Science, University of California, Los Angeles, USA;
This paper is
[5] If such nodes exist, we can always collapse them into a single sum or product node.