Abstract

1 Introduction

2 Related Work

3 The Seven Qualification Tests for an AI Scientist

4 Discussions

5 Conclusions and Future Work and References

3 The Seven Qualification Tests for an AI Scientist

3 The Seven Qualification Tests for an AI Scientist

3.1 Selection Criteria

An ideal “Turing” test for an AI scientist should satisfy the following three criteria:

  1. It is the key to an important discovery in the development of science.
  2. It is possible to be discovered digitally, without interaction with the physical world.
  3. The discovery is possible based on data or interaction within a well-defined scope (such as a dataset or a set of interactive libraries). The first two criteria are straight-forward, and here we explain why we need the third criterion. Each important scientific discovery has deep impact in our civilization, and may have become common sense (e.g., the earth orbits the sun). Both the discovery itself and the facts and technologies depending on it can be documented here and there in our written corpus. It is impossible to create a generic training set for a model without including such knowledge. Therefore, we have to confine the scope of the data and/or interactive tools an AI can access, to avoid any possible information leak. Table 1 summarizes our seven tests and their significance in the history of science. We do not select any test from many most important disciplines, such as chemistry, biology, and geology, because they either require interacting with the physical world or have a limited amount of observations.

3.2 The Heliocentric Model Test

The exploration of the night sky was pivotal in the evolution to modern scientific methods, primarily driven by the contributions of astronomers like Johannes Kepler and Galileo Galilei. Kepler’s laws of planetary motion, derived from his observations, established the foundation for the heliocentric solar system model, paving the way for Newton’s theory of gravity. Similarly, Galileo’s approach of blending experimental data with mathematical analysis became a fundamental element of the scientific method, earning him the title ”Father of Modern Science.” Thus, a suitable initial ”Turing test” for an AI scientist might involve rediscovery of the heliocentric model using only observations of the night sky. This would require an AI to derive laws that govern celestial motion and integrate these into a mathematical model, including making revolutionary conjectures, such as suggesting Earth and other celestial bodies have similar properties. For such a test to effectively assess an AI scientist, it should involve a vast dataset and/or an interactive environment. For instance, the position of celestial bodies at specific times could be determined using the AstroPy library[7]. Here is our first test, the Heliocentric Model Test: Given an interactive Python library like AstroPy, which provides the coordinates of any observable celestial objects at any moment, the test would see if an AI agent can derive Kepler’s three laws and acknowledge that planets orbit the sun. An additional challenge could involve recognizing that Earth orbits the sun, although it is optional. Here is an example of using AstroPy to get the location of a celestial object at a certain moment.

3.3 The Motion Laws Test

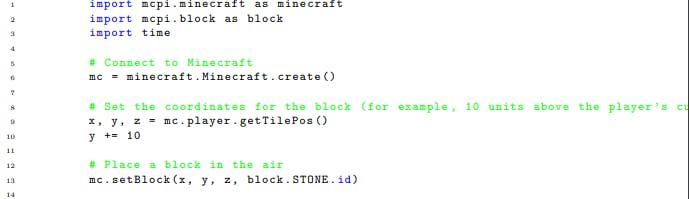
Our second test, Motion Laws Test, aims at rediscovering the fundamental principles of motion. It is non-trivial for an AI agent to interact with the real world objects. Fortunately the virtual worlds such as Minecraft offers a platform for exploration in kinetics. This test would assess the AI’s ability to derive the Law of Inertia, and the Law of Acceleration under the influence of gravity, solely from interactions and observations within the game and a few mathematics tools such as PySR and SymPy. In this test, the AI would need to manipulate and measure the dynamics of various objects under different conditions within the game. For example, the AI could alter the mass of blocks, apply forces, and observe the trajectories. By analyzing these observations (using tools such as PySR and SymPy), the AI would need to derive the formula corresponding to the Law of Inertia and the Law of Acceleration due to gravity. One can use Minecraft: Pi edition API Python Library[10] to control objects in Minecraft in Python. As shown in the example below, one can set a block in the air and observe its position after one second.

3.4 The Vibrating Strings Test

The problem of vibrating strings significantly influenced the development of differential equations during the 17th and 18th centuries, especially in the context of music and acoustics. In his seminal work in 1747, Jean le Rond d’Alembert formulated the onedimensional wave equation to describe the motion of a vibrating string. This equation, expressed in trigonometric functions, suggested that the string’s vibrations could be depicted as a sum of sinusoidal waves of various frequencies and amplitudes. The intense debate on the correct solution to the vibrating string problem among mathematicians like Daniel Bernoulli and Leonhard Euler fueled advances in differential equations. Bernoulli’s advocacy for representing vibrations as a series of harmonic motions led to the principle of superposition in wave theory, while Euler explored different boundary conditions. Their collective efforts advanced the field of differential equations by developing techniques like separation of variables, and applied these methods to practical mechanics and beyond. In the Vibrating Strings Test, an AI agent would be assessed by its capability to derive the simple and elegant different equation for vibrating strings:

where u(x, t) is the displacement of the string, t is time, and x is the spatial coordinate along the string. It is not required for the AI to infer that c is the speed of wave propagation in the string, and the AI can replace c 2 with a positive constant. Please note the AI is not allowed to use prior knowledge about calculus, because that would reduce this problem to a simple symbolic regression on second derivatives. Instead, we expect the AI to discover the concept of ”differentiation” on it own, possibly through exploring a large variety of possible concepts. One can use the python package for simulating vibrating strings in [20] to create infinite examples, which should allow the AI to apply all kinds of hypotheses, in order to discover the simplest one that is consistent with the observations.

3.5 The Maxwell’s Equations Test

Since proposed in 1862, Maxwell’s equations have been celebrated for their mathematical elegance, encapsulating the fundamentals of electromagnetism in a set of concise, interrelated equations. Here are the four equations formed as differential equations: Gauss’s Law for Electricity:

3.6 The Initial Value Problem Test

An initial value problem (IVP) involves solving a differential equation subject to specific initial conditions. The development of IVP, particularly in the context of differential equations, is a cornerstone of modern numerical computing. During the 18th and 19th centuries, mathematicians like Leonhard Euler, Joseph-Louis Lagrange, and Carl Friedrich Gauss further developed methods to solve differential equations arising in physics and astronomy. Euler’s method, developed in the 1760s, is one of the earliest numerical methods for solving initial value problems. Consider the initial value problem (IVP) for the differential equation:

Here k1, k2, k3 and k4 are intermediate values used to calculate yn+1, which is the next approximation of the solution. Please note this is the fourth-order Runge-Kutta method, meaning its global truncation error is of the order O(h 4 ), where h is the step size. One can choose Runge-Kutta methods (or alternatives) with higher orders, which usually have lower errors. In the Initial Value Problem Test, an AI is assessed by its capability in inventing a numerical method that is at least as precise as the fourth-order Runge-Kutta method. This probably requires the AI to go beyond simple try and error, and learn from its own exploration (e.g., with reinforcement learning).

3.7 The Huffman Coding Test

Huffman coding[14] is a most important piece of work in information theory. It generates variable-length codes where each code’s length is inversely proportional to the likelihood of the symbol it represents. This aligns directly with Shannon’s source coding theorem[23], a fundamental principle in information theory. The theorem states that in an optimal code, the average length of the symbols should be close to the entropy of the source. Huffman coding achieves this by ensuring that the most frequent symbols have the shortest codes, thereby minimizing the overall expected code length needed to represent each symbol. Our sixth test is the Huffman Coding Test. Given a large corpus of ascii characters, and Python functions to operate on bits, check if an AI agent can discover Huffman coding when working towards the goal of minimizing storage under the constraint that each character be represented by a specific sequence of 0’s and 1’s. Given the above constraint, an AI could create many random assignments of codes for various characters. It then needs to discover the Prefix-free Property (i.e., no code is a prefix of another code), in order to create valid codings. Then it needs to observe the efficiency of each coding, and learns from the exploration of various codings.

3.8 The Sorting Algorithm Test

Sorting is probably the most studied problem in computer science, with numerous great algorithms proposed. Given a very large set of examples (e.g., arrays of integers and the sorted version of them), it should be trivial for a large model to be trained to generate the sorted array based on the original array. However, a black-box model is not what we want. Our goal is to develop an efficient sorting algorithm that can run on a simple single-threaded manner. Our last test is the Sorting Algorithm Test, which assesses whether an AI can come up with a sorting function in Python that runs in expected O(nlogn) time, given a very large number of examples of sorting integer arrays. To avoid leaking the answer, the AI should not be aware of any human-written programs. However, it should know Python’s syntax and be able to generate valid (but random) Python code, without understanding its meaning. One possible route is to let the AI generate a huge number of random Python code and run them on the given arrays. In this way it should be able to learn what kind of code converts an array into another array. Then it can generate a huge number of such random Python functions, and observes which of them can successfully sort a (possibly small) input array. As it keeps learning from its exploration, it should be able to generate various types of sorting functions. Its final step should be learn to predict the running time of each sorting function, in order to generate more efficient algorithms.

Authors:

  1. Xiaoxin Yin

This paper is available on arxiv under CC by 4.0 Deed (Attribution 4.0 International) license.