Content Overview

Indexing

Ragged tensors support Python-style indexing, including multidimensional indexing and slicing. The following examples demonstrate ragged tensor indexing with a 2D and a 3D ragged tensor.

Indexing examples: 2D ragged tensor

queries = tf.ragged.constant(
    [['Who', 'is', 'George', 'Washington'],
     ['What', 'is', 'the', 'weather', 'tomorrow'],
     ['Goodnight']])


print(queries[1])                   # A single query


tf.Tensor([b'What' b'is' b'the' b'weather' b'tomorrow'], shape=(5,), dtype=string)


print(queries[1, 2])                # A single word


tf.Tensor(b'the', shape=(), dtype=string)


print(queries[1:])                  # Everything but the first row


<tf.RaggedTensor [[b'What', b'is', b'the', b'weather', b'tomorrow'], [b'Goodnight']]><tf.RaggedTensor [[b'What', b'is', b'the', b'weather', b'tomorrow'], [b'Goodnight']]>


print(queries[:, :3])               # The first 3 words of each query


<tf.RaggedTensor [[b'Who', b'is', b'George'], [b'What', b'is', b'the'], [b'Goodnight']]>


print(queries[:, -2:])              # The last 2 words of each query


<tf.RaggedTensor [[b'George', b'Washington'], [b'weather', b'tomorrow'], [b'Goodnight']]>

Indexing examples: 3D ragged tensor

rt = tf.ragged.constant([[[1, 2, 3], [4]],
                         [[5], [], [6]],
                         [[7]],
                         [[8, 9], [10]]])


print(rt[1])                        # Second row (2D RaggedTensor)


<tf.RaggedTensor [[5], [], [6]]>


print(rt[3, 0])                     # First element of fourth row (1D Tensor)


tf.Tensor([8 9], shape=(2,), dtype=int32)


print(rt[:, 1:3])                   # Items 1-3 of each row (3D RaggedTensor)


<tf.RaggedTensor [[[4]], [[], [6]], [], [[10]]]>


print(rt[:, -1:])                   # Last item of each row (3D RaggedTensor)


<tf.RaggedTensor [[[4]],

 [[6]],

 [[7]],

 [[10]]]>

RaggedTensors support multidimensional indexing and slicing with one restriction: indexing into a ragged dimension is not allowed. This case is problematic because the indicated value may exist in some rows but not others. In such cases, it's not obvious whether you should (1) raise an IndexError; (2) use a default value; or (3) skip that value and return a tensor with fewer rows than you started with. Following the guiding principles of Python ("In the face of ambiguity, refuse the temptation to guess"), this operation is currently disallowed.

Tensor type conversion

The RaggedTensor class defines methods that can be used to convert between RaggedTensors and tf.Tensors or tf.SparseTensors:

ragged_sentences = tf.ragged.constant([
    ['Hi'], ['Welcome', 'to', 'the', 'fair'], ['Have', 'fun']])


# RaggedTensor -> Tensor
print(ragged_sentences.to_tensor(default_value='', shape=[None, 10]))


tf.Tensor(
[[b'Hi' b'' b'' b'' b'' b'' b'' b'' b'' b'']
 [b'Welcome' b'to' b'the' b'fair' b'' b'' b'' b'' b'' b'']
 [b'Have' b'fun' b'' b'' b'' b'' b'' b'' b'' b'']], shape=(3, 10), dtype=string)


# Tensor -> RaggedTensor
x = [[1, 3, -1, -1], [2, -1, -1, -1], [4, 5, 8, 9]]
print(tf.RaggedTensor.from_tensor(x, padding=-1))


<tf.RaggedTensor [[1, 3], [2], [4, 5, 8, 9]]>


#RaggedTensor -> SparseTensor
print(ragged_sentences.to_sparse())


SparseTensor(indices=tf.Tensor(
[[0 0]
 [1 0]
 [1 1]
 [1 2]
 [1 3]
 [2 0]
 [2 1]], shape=(7, 2), dtype=int64), values=tf.Tensor([b'Hi' b'Welcome' b'to' b'the' b'fair' b'Have' b'fun'], shape=(7,), dtype=string), dense_shape=tf.Tensor([3 4], shape=(2,), dtype=int64))


# SparseTensor -> RaggedTensor
st = tf.SparseTensor(indices=[[0, 0], [2, 0], [2, 1]],
                     values=['a', 'b', 'c'],
                     dense_shape=[3, 3])
print(tf.RaggedTensor.from_sparse(st))


<tf.RaggedTensor [[b'a'], [], [b'b', b'c']]>

Evaluating ragged tensors

To access the values in a ragged tensor, you can:

  1. Use tf.RaggedTensor.to_list to convert the ragged tensor to a nested Python list.
  2. Use tf.RaggedTensor.numpy to convert the ragged tensor to a NumPy array whose values are nested NumPy arrays.
  3. Decompose the ragged tensor into its components, using the tf.RaggedTensor.values and tf.RaggedTensor.row_splits properties, or row-partitioning methods such as tf.RaggedTensor.row_lengths and tf.RaggedTensor.value_rowids.
  4. Use Python indexing to select values from the ragged tensor.

rt = tf.ragged.constant([[1, 2], [3, 4, 5], [6], [], [7]])
print("Python list:", rt.to_list())
print("NumPy array:", rt.numpy())
print("Values:", rt.values.numpy())
print("Splits:", rt.row_splits.numpy())
print("Indexed value:", rt[1].numpy())


Python list: [[1, 2], [3, 4, 5], [6], [], [7]]
NumPy array: [array([1, 2], dtype=int32) array([3, 4, 5], dtype=int32)
 array([6], dtype=int32) array([], dtype=int32) array([7], dtype=int32)]
Values: [1 2 3 4 5 6 7]
Splits: [0 2 5 6 6 7]
Indexed value: [3 4 5]

Ragged Shapes

The shape of a tensor specifies the size of each axis. For example, the shape of [[1, 2], [3, 4], [5, 6]] is [3, 2], since there are 3 rows and 2 columns. TensorFlow has two separate but related ways to describe shapes:

Static shape

A Tensor's static shape contains information about its axis sizes that is known at graph-construction time. For both tf.Tensor and tf.RaggedTensor, it is available using the .shape property, and is encoded using tf.TensorShape:

x = tf.constant([[1, 2], [3, 4], [5, 6]])
x.shape  # shape of a tf.tensor


TensorShape([3, 2])


rt = tf.ragged.constant([[1], [2, 3], [], [4]])
rt.shape  # shape of a tf.RaggedTensor


TensorShape([4, None])

The static shape of a ragged dimension is always None (i.e., unspecified). However, the inverse is not true -- if a TensorShape dimension is None, then that could indicate that the dimension is ragged, or it could indicate that the dimension is uniform but that its size is not statically known.

Dynamic shape

A tensor's dynamic shape contains information about its axis sizes that is known when the graph is run. It is constructed using the tf.shape operation. For tf.Tensor, tf.shape returns the shape as a 1D integer Tensor, where tf.shape(x)[i] is the size of axis i.

x = tf.constant([['a', 'b'], ['c', 'd'], ['e', 'f']])
tf.shape(x)


<tf.Tensor: shape=(2,), dtype=int32, numpy=array([3, 2], dtype=int32)>

However, a 1D Tensor is not expressive enough to describe the shape of a tf.RaggedTensor. Instead, the dynamic shape for ragged tensors is encoded using a dedicated type, tf.experimental.DynamicRaggedShape. In the following example, the DynamicRaggedShape returned by tf.shape(rt) indicates that the ragged tensor has 4 rows, with lengths 1, 3, 0, and 2:

rt = tf.ragged.constant([[1], [2, 3, 4], [], [5, 6]])
rt_shape = tf.shape(rt)
print(rt_shape)


<DynamicRaggedShape lengths=[4, (1, 3, 0, 2)] num_row_partitions=1>

Dynamic shape: operations

DynamicRaggedShapes can be used with most TensorFlow ops that expect shapes, including tf.reshape, tf.zeros, tf.ones. tf.fill, tf.broadcast_dynamic_shape, and tf.broadcast_to.

print(f"tf.reshape(x, rt_shape) = {tf.reshape(x, rt_shape)}")
print(f"tf.zeros(rt_shape) = {tf.zeros(rt_shape)}")
print(f"tf.ones(rt_shape) = {tf.ones(rt_shape)}")
print(f"tf.fill(rt_shape, 9) = {tf.fill(rt_shape, 'x')}")


tf.reshape(x, rt_shape) = <tf.RaggedTensor [[b'a'], [b'b', b'c', b'd'], [], [b'e', b'f']]>
tf.zeros(rt_shape) = <tf.RaggedTensor [[0.0], [0.0, 0.0, 0.0], [], [0.0, 0.0]]>
tf.ones(rt_shape) = <tf.RaggedTensor [[1.0], [1.0, 1.0, 1.0], [], [1.0, 1.0]]>
tf.fill(rt_shape, 9) = <tf.RaggedTensor [[b'x'], [b'x', b'x', b'x'], [], [b'x', b'x']]>

Dynamic shape: indexing and slicing

DynamicRaggedShape can be also be indexed to get the sizes of uniform dimensions. For example, we can find the number of rows in a raggedtensor using tf.shape(rt)[0] (just as we would for a non-ragged tensor):

rt_shape[0]


<tf.Tensor: shape=(), dtype=int32, numpy=4>

However, it is an error to use indexing to try to retrieve the size of a ragged dimension, since it doesn't have a single size. (Since RaggedTensor keeps track of which axes are ragged, this error is only thrown during eager execution or when tracing a tf.function; it will never be thrown when executing a concrete function.)

try:
  rt_shape[1]
except ValueError as e:
  print("Got expected ValueError:", e)


Got expected ValueError: Index 1 is not uniform

DynamicRaggedShapes can also be sliced, as long as the slice either begins with axis 0, or contains only dense dimensions.

rt_shape[:1]


<DynamicRaggedShape lengths=[4] num_row_partitions=0>

Dynamic shape: encoding

DynamicRaggedShape is encoded using two fields:

For more information about row partitions, see the "RaggedTensor encoding" section below, and the API docs for tf.experimental.RowPartition.

Dynamic shape: construction

DynamicRaggedShape is most often constructed by applying tf.shape to a RaggedTensor, but it can also be constructed directly:

tf.experimental.DynamicRaggedShape(
    row_partitions=[tf.experimental.RowPartition.from_row_lengths([5, 3, 2])],
    inner_shape=[10, 8])


<DynamicRaggedShape lengths=[3, (5, 3, 2), 8] num_row_partitions=1>

If the lengths of all rows are known statically, DynamicRaggedShape.from_lengths can also be used to construct a dynamic ragged shape. (This is mostly useful for testing and demonstration code, since it's rare for the lengths of ragged dimensions to be known statically).

tf.experimental.DynamicRaggedShape.from_lengths([4, (2, 1, 0, 8), 12])


<DynamicRaggedShape lengths=[4, (2, 1, 0, 8), 12] num_row_partitions=1>

Broadcasting

Broadcasting is the process of making tensors with different shapes have compatible shapes for elementwise operations. For more background on broadcasting, refer to:

The basic steps for broadcasting two inputs x and y to have compatible shapes are:

  1. If x and y do not have the same number of dimensions, then add outer dimensions (with size 1) until they do.
  2. For each dimension where x and y have different sizes:

Where the size of a tensor in a uniform dimension is a single number (the size of slices across that dimension); and the size of a tensor in a ragged dimension is a list of slice lengths (for all slices across that dimension).

Broadcasting examples

# x       (2D ragged):  2 x (num_rows)
# y       (scalar)
# result  (2D ragged):  2 x (num_rows)
x = tf.ragged.constant([[1, 2], [3]])
y = 3
print(x + y)


<tf.RaggedTensor [[4, 5], [6]]>


# x         (2d ragged):  3 x (num_rows)
# y         (2d tensor):  3 x          1
# Result    (2d ragged):  3 x (num_rows)
x = tf.ragged.constant(
   [[10, 87, 12],
    [19, 53],
    [12, 32]])
y = [[1000], [2000], [3000]]
print(x + y)


<tf.RaggedTensor [[1010, 1087, 1012], [2019, 2053], [3012, 3032]]>


# x      (3d ragged):  2 x (r1) x 2
# y      (2d ragged):         1 x 1
# Result (3d ragged):  2 x (r1) x 2
x = tf.ragged.constant(
    [[[1, 2], [3, 4], [5, 6]],
     [[7, 8]]],
    ragged_rank=1)
y = tf.constant([[10]])
print(x + y)


<tf.RaggedTensor [[[11, 12],
  [13, 14],
  [15, 16]], [[17, 18]]]>


# x      (3d ragged):  2 x (r1) x (r2) x 1
# y      (1d tensor):                    3
# Result (3d ragged):  2 x (r1) x (r2) x 3
x = tf.ragged.constant(
    [
        [
            [[1], [2]],
            [],
            [[3]],
            [[4]],
        ],
        [
            [[5], [6]],
            [[7]]
        ]
    ],
    ragged_rank=2)
y = tf.constant([10, 20, 30])
print(x + y)


<tf.RaggedTensor [[[[11, 21, 31],
   [12, 22, 32]], [], [[13, 23, 33]], [[14, 24, 34]]],
 [[[15, 25, 35],
   [16, 26, 36]], [[17, 27, 37]]]]>

Here are some examples of shapes that do not broadcast:

# x      (2d ragged): 3 x (r1)
# y      (2d tensor): 3 x    4  # trailing dimensions do not match
x = tf.ragged.constant([[1, 2], [3, 4, 5, 6], [7]])
y = tf.constant([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
try:
  x + y
except tf.errors.InvalidArgumentError as exception:
  print(exception)


Condition x == y did not hold.
Indices of first 3 different values:
[[1]
 [2]
 [3]]
Corresponding x values:
[ 4  8 12]
Corresponding y values:
[2 6 7]
First 3 elements of x:
[0 4 8]
First 3 elements of y:
[0 2 6]


# x      (2d ragged): 3 x (r1)
# y      (2d ragged): 3 x (r2)  # ragged dimensions do not match.
x = tf.ragged.constant([[1, 2, 3], [4], [5, 6]])
y = tf.ragged.constant([[10, 20], [30, 40], [50]])
try:
  x + y
except tf.errors.InvalidArgumentError as exception:
  print(exception)


Condition x == y did not hold.
Indices of first 2 different values:
[[1]
 [3]]
Corresponding x values:
[3 6]
Corresponding y values:
[2 5]
First 3 elements of x:
[0 3 4]
First 3 elements of y:
[0 2 4]


# x      (3d ragged): 3 x (r1) x 2
# y      (3d ragged): 3 x (r1) x 3  # trailing dimensions do not match
x = tf.ragged.constant([[[1, 2], [3, 4], [5, 6]],
                        [[7, 8], [9, 10]]])
y = tf.ragged.constant([[[1, 2, 0], [3, 4, 0], [5, 6, 0]],
                        [[7, 8, 0], [9, 10, 0]]])
try:
  x + y
except tf.errors.InvalidArgumentError as exception:
  print(exception)


Condition x == y did not hold.
Indices of first 3 different values:
[[1]
 [2]
 [3]]
Corresponding x values:
[2 4 6]
Corresponding y values:
[3 6 9]
First 3 elements of x:
[0 2 4]
First 3 elements of y:
[0 3 6]

RaggedTensor encoding

Ragged tensors are encoded using the RaggedTensor class. Internally, each RaggedTensor consists of:

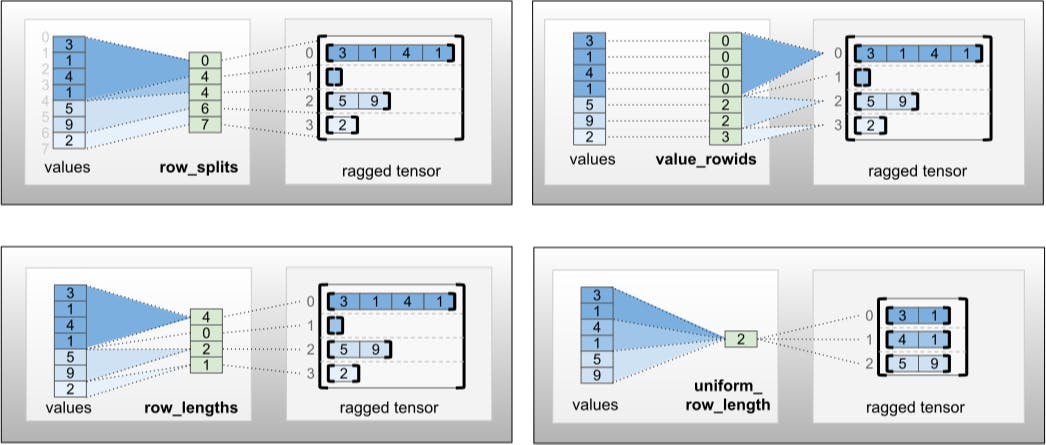
The row_partition can be stored using four different encodings:

An integer scalar nrows can also be included in the row_partition encoding to account for empty trailing rows with value_rowids or empty rows with uniform_row_length.

rt = tf.RaggedTensor.from_row_splits(
    values=[3, 1, 4, 1, 5, 9, 2],
    row_splits=[0, 4, 4, 6, 7])
print(rt)


<tf.RaggedTensor [[3, 1, 4, 1], [], [5, 9], [2]]>

The choice of which encoding to use for row partitions is managed internally by ragged tensors to improve efficiency in some contexts. In particular, some of the advantages and disadvantages of the different row-partitioning schemes are:

Multiple ragged dimensions

A ragged tensor with multiple ragged dimensions is encoded by using a nested RaggedTensor for the values tensor. Each nested RaggedTensor adds a single ragged dimension.

rt = tf.RaggedTensor.from_row_splits(
    values=tf.RaggedTensor.from_row_splits(
        values=[10, 11, 12, 13, 14, 15, 16, 17, 18, 19],
        row_splits=[0, 3, 3, 5, 9, 10]),
    row_splits=[0, 1, 1, 5])
print(rt)
print("Shape: {}".format(rt.shape))
print("Number of partitioned dimensions: {}".format(rt.ragged_rank))


<tf.RaggedTensor [[[10, 11, 12]], [], [[], [13, 14], [15, 16, 17, 18], [19]]]>
Shape: (3, None, None)
Number of partitioned dimensions: 2

The factory function tf.RaggedTensor.from_nested_row_splits may be used to construct a RaggedTensor with multiple ragged dimensions directly by providing a list of row_splits tensors:

rt = tf.RaggedTensor.from_nested_row_splits(
    flat_values=[10, 11, 12, 13, 14, 15, 16, 17, 18, 19],
    nested_row_splits=([0, 1, 1, 5], [0, 3, 3, 5, 9, 10]))
print(rt)


<tf.RaggedTensor [[[10, 11, 12]], [], [[], [13, 14], [15, 16, 17, 18], [19]]]>

Ragged rank and flat values

A ragged tensor's ragged rank is the number of times that the underlying values tensor has been partitioned (i.e. the nesting depth of RaggedTensor objects). The innermost values tensor is known as its flat_values. In the following example, conversations has ragged_rank=3, and its flat_values is a 1D Tensor with 24 strings:

# shape = [batch, (paragraph), (sentence), (word)]
conversations = tf.ragged.constant(
    [[[["I", "like", "ragged", "tensors."]],
      [["Oh", "yeah?"], ["What", "can", "you", "use", "them", "for?"]],
      [["Processing", "variable", "length", "data!"]]],
     [[["I", "like", "cheese."], ["Do", "you?"]],
      [["Yes."], ["I", "do."]]]])
conversations.shape


TensorShape([2, None, None, None])


assert conversations.ragged_rank == len(conversations.nested_row_splits)
conversations.ragged_rank  # Number of partitioned dimensions.


3


conversations.flat_values.numpy()


array([b'I', b'like', b'ragged', b'tensors.', b'Oh', b'yeah?', b'What',
       b'can', b'you', b'use', b'them', b'for?', b'Processing',
       b'variable', b'length', b'data!', b'I', b'like', b'cheese.', b'Do',
       b'you?', b'Yes.', b'I', b'do.'], dtype=object)

Uniform inner dimensions

Ragged tensors with uniform inner dimensions are encoded by using a multidimensional tf.Tensor for the flat_values (i.e., the innermost values).

rt = tf.RaggedTensor.from_row_splits(
    values=[[1, 3], [0, 0], [1, 3], [5, 3], [3, 3], [1, 2]],
    row_splits=[0, 3, 4, 6])
print(rt)
print("Shape: {}".format(rt.shape))
print("Number of partitioned dimensions: {}".format(rt.ragged_rank))
print("Flat values shape: {}".format(rt.flat_values.shape))
print("Flat values:\n{}".format(rt.flat_values))


<tf.RaggedTensor [[[1, 3],
  [0, 0],
  [1, 3]], [[5, 3]], [[3, 3],
                      [1, 2]]]>
Shape: (3, None, 2)
Number of partitioned dimensions: 1
Flat values shape: (6, 2)
Flat values:
[[1 3]
 [0 0]
 [1 3]
 [5 3]
 [3 3]
 [1 2]]

Uniform non-inner dimensions

Ragged tensors with uniform non-inner dimensions are encoded by partitioning rows with uniform_row_length.

rt = tf.RaggedTensor.from_uniform_row_length(
    values=tf.RaggedTensor.from_row_splits(
        values=[10, 11, 12, 13, 14, 15, 16, 17, 18, 19],
        row_splits=[0, 3, 5, 9, 10]),
    uniform_row_length=2)
print(rt)
print("Shape: {}".format(rt.shape))
print("Number of partitioned dimensions: {}".format(rt.ragged_rank))


<tf.RaggedTensor [[[10, 11, 12], [13, 14]],
 [[15, 16, 17, 18], [19]]]>
Shape: (2, 2, None)
Number of partitioned dimensions: 2

Originally published on the TensorFlow website, this article appears here under a new headline and is licensed under CC BY 4.0. Code samples shared under the Apache 2.0 License.