Theoretical Memory Efficiency Gains with LoRA for Single and Multi-GPU Settings

Table of Links

Abstract and 1 Introduction

2 Background

3 Experimental Setup and 3.1 Datasets for Continued Pretraining (CPT) and Instruction Finetuning (IFT)

3.2 Measuring Learning with Coding and Math Benchmarks (target domain evaluation)

3.3 Forgetting Metrics (source domain evaluation)

4 Results

4.1 LoRA underperforms full finetuning in programming and math tasks

4.2 LoRA forgets less than full finetuning

4.3 The Learning-Forgetting Tradeoff

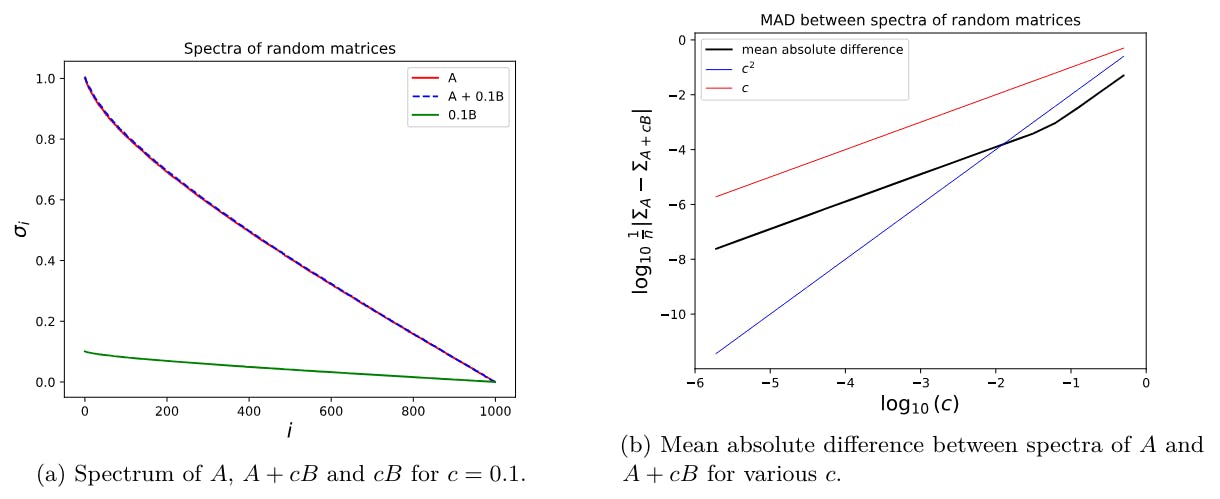
4.4 LoRA’s regularization properties

4.5 Full finetuning on code and math does not learn low-rank perturbations

4.6 Practical takeaways for optimally configuring LoRA

5 Related Work

6 Discussion

7 Conclusion and References

Appendix

A. Experimental Setup

B. Learning rate searches

C. Training Datasets

D. Theoretical Memory Efficiency Gains with LoRA for Single and Multi-GPU Settings

D Theoretical Memory Efficiency Gains with LoRA for Single and Multi-GPU Settings

Modern systems for training neural networks store and operate on the following objects (following the conventions in Rajbhandari et al. (2020)). Most memory requirements relate to model states, which include:

• parameter weights

• gradients

• higher order optimization quantities such as optimizer momentum and variance in the Adam optimizer, and the momentum in the Lion optimizer

The remaining memory requirements come from the residual states:

• activations (which depend on batch size and maximum sample sequence length)

• temporary buffers for intermediate quantities in the forward and backward pass.

which will require more memory when increasing the batch size and maximum sequence lengths.

LoRA offers memory savings with respect to the model states. The next two sections describe these memory savings in the single GPU and multi-GPU setting with examples loosely inspired by Rajbhandari et al. (2020).

The data stored at single precision includes:

• a “master copy” of the tuned parameter weights

• the gradient

• all optimizer states (both momentum and variance for Adam, and just momentum for Lion)

For simplicity, we do not consider mixed-precision training, which involves storing critical data at single precision (fp32; 4 bytes per number) while performing some computations at half precision (fp16 or bfloat16; 2 bytes per number).

D.1 Training on a Single GPU

In the single GPU setup, the difference in memory requirements between LoRA and full finetuning is particularly drastic when using the Adam optimizer (Hu et al., 2021; Rajbhandari et al., 2020).

Storing the master weights in fp32 requires 4 bytes per parameter, while storing the gradient in fp32 requires 4 bytes per tuned parameter. In order to maintain the optimizer state in fp32 for Adam, 8 bytes per tuned parameter are required; 4 bytes for the momentum term, and 4 bytes for the variance term. Let Ψ be the number of model parameters. Therefore, in the Adam full finetuning setting of a Ψ = 7B parameter model, the total memory requirements are at least roughly 4 × Ψ + 4 × Ψ + 8 × Ψ = 112 GB.

The Lion optimizer only uses a momentum term in the gradient calculation, and the variance term in Adam therefore disappears. In the Lion full finetuning setting of a Ψ = 7B parameter model, the total memory requirements are therefore roughly 4 × Ψ + 4 × Ψ + 4 × Ψ = 84 GB.

LoRA, on the other hand, does not calculate the gradients or maintain optimizer states (momentum and variance terms) for most of the parameters. Therefore the amount of memory used for these terms is drastically reduced.

A LoRA setting with Adam that only tunes matrices that are 1% of the total parameter count (e.g. Ψ = 7B base model with 70M additional parameters used by LoRA) requires roughly 4 × Ψ(1 + 0.01) + 4 × Ψ × 0.01 + 8 × Ψ × 0.01 = 29.12 GB of memory. Theoretically this can be reduced further to 2 × Ψ + 16 × Ψ × 0.01 = 15.12 GB if the non-tuned parameter weights are stored in bfloat16. We use this assumption for the subsequent examples.

Note again that these numbers do not take into consideration sample batch size or sequence length, which affect the memory requirements of the activations.

D.2 Training on a Multiple with Fully Sharded Data Parallelism

Past approaches for training LLMs across multiple GPUs include model parallelism, where different layers of the LLM are stored on different GPUs. However this requires high communication overhead and has very poor throughput (Rajbhandari et al., 2020). Fully Sharded Data Parallelism (FSDP) shards the parameters, the gradient, and the optimizer states across GPUs. This incredibly efficient and actually is competitive with the memory savings offered by LoRA in certain settings.

FSDP sharding the parameter and optimizer states across N devices results in less memory usage relative to LoRA. LoRA on the other hand enables training on GPUs with far less memory and also emanes training without needing as many GPUs to shard across.

For example, in the Adam full finetuning setting of a Ψ = 7B parameter model on 8 GPUs with FSDP, the total memory requirement for each GPU is roughly (4 × Ψ + 4 × Ψ + 8 × Ψ)/8 = 14 GB. This reduces further to 3.5 GB for FSDP with 32 GPUs (see Table S1).

The LoRA with Adam setup on 8 GPUs (where Ψ = 7B base model and there are 70M additional LoRA parameters) requires roughly (2 × Ψ + 16 × Ψ × 0.01)/8 = 1.89 GB of memory per GPU. With 32 GPUs this decreases further to 0.4725 GB.

Standard industry level GPUs have on-device memory between 16 GB (e.g. V100s) and 80 GB (e.g. A100s and H100s). As Table S1 demonstrates, the per-GPU memory requirements for training a 7B parameter model decrease drastically as the number of GPUs increase. The memory requirements for training a 7B model with Adam + LoRA on a single GPU are 15.12 GB, but the same per-GPU memory requirement for training a 7B model with Adam but without LoRA on 8 GPUs is 14 GB. In this 8 GPU scenario, the efficiency gains from LoRA disappear.

Table S2 applies similar calculations to a 70B parameter model. Finetuning such a large model on 8 GPUs is only possible using a technique like LoRA; where Adam requires 140 GB per GPU, Adam+LoRA requires 18.9 GB per GPU. The efficiency gains of LoRA relative to FSDP therefore depend on the model size and GPU availability/cost considerations.

We do the same analysis for a 405B parameter model to highlight how LoRA is beneficial as model size scales (Table S3).