Why Public-Key Encryption Will Never Be 100% Secure

Table of Links

Abstract and 1 Introduction

2. Scenario and Requirements

3. History and Related Work

4. Concept of Cramer-Shoup with Elliptic Curve and 4.1 Prerequisite

   4.2 Public Key Generation by Receiver

   4.3 Encryption by Sender

   4.4 Decryption by Receiver

5. Evaluation and 5.1 Proof of Correctness

   5.2 Preliminary Performance Comparison

6. Proof: Secure against adaptive-chosen ciphertext attacks

   6.1 DDH Assumption and 6.2 CCA Assumption

   6.3 IND-CCA 1 - non-adaptive Security

   6.4 IND-CCA 2 - adaptive Security (Validity Checking Failure)

7. Security discussion: Post-Quantum Cryptography

8. Summary, References, and Authors

3 History and Related Work

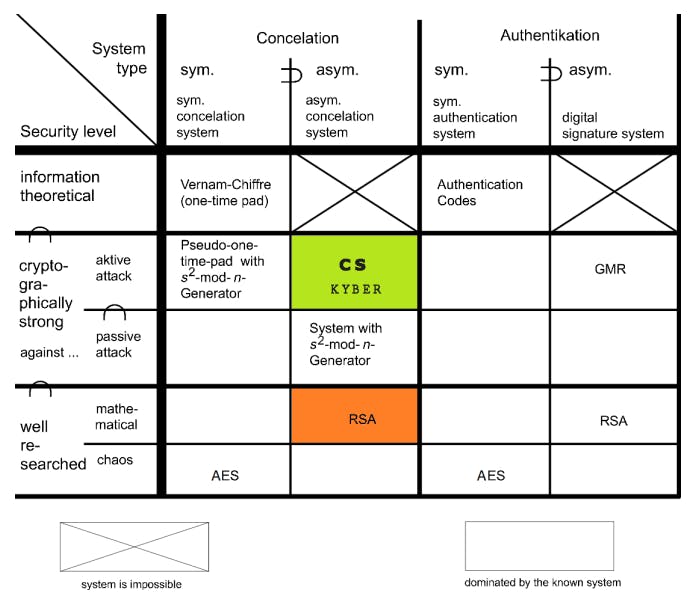
Advances in quantum computing have created a need for new methods in PQC. Over the past years, different cryptography systems have been developed. Many schema can be used and combined for multiple security operations. An overview about established cryptographic systems and their security level is given in Figure 2. It shows the theoretical limits for their level of security in the different categories. As this publication focus on publickey encryption, the highest security level can only be cryptographic strong. A public-key crypto system can never be information theoretical secure due to the public-key testing possibility. The following list of encryption methods illustrates the known security levels based on their historical development. One of the first public-key crypto systems was developed by Ralph Merkle with the Merkle Puzzle, later published in 1978 [17]. Nevertheless, James H. Ellis, Clifford Cocks, and Malcolm Williamson invented public-key cryptography for the British Government Communications Headquarters in 1970 [18]. The first wide spread protocol for asymmetric cryptography is the Diffie–Hellman(-Merkle) (DH) key exchange for a non-authenticated key-agreement, since 1976 [19]. Beyond that, the first public-key scheme was developed by Rivest, Shamir und Adleman (RSA) at the Massachusetts Institute of Technology in 1977 [20]. These are based on the assumption of the hardness of the factoring problem or discrete logarithm problem (DLP). Since these systems work deterministic, it is susceptible to simple attacks. Therefore, for example RSA has to be combined with OAEP in practice nowadays [2]. The unmodified RSA is not indistinguishable for chosen plain-text attacks (IND-CPA), which is mandatory for current systems. Beside these, there are many more Public-Key schemes with the following security problems (excerpt):

– Merkle-Hellman [21]: Trapdoor knapsacks; broken [22].

– McEliece [23]: Provable hardness of decoding a general linear code (IND-CPA); proposed PQC; comparable large keys.

– Rabin [24]: Provable for factoring problem; 4-to-1 output, which leads to decryption failure.

– Chor-Rivest [25]: no feasible attack known; comparable large key.

– Elgamal [26]: Provable hardness of decisional Diffie–Hellman assumption (IND-CPA); malleable.

– NTRUEncrypt [27]: Provable hardness for correctness Ring Learning with Errors; proposed PQC; comparable large keys.

– Paillier [28]: Provable hardness of decisional composite residuosity problem (INDCPA); malleable.

American NIST and European ENISA are currently running a competition for new methods for quantum-resistant public-key cryptographic [29,30,31]. CRYSTALS-Kyber has been nominated as a possible finalist [32,33]. Contrary to our EC or Isogeny approach, Kyber is based on the hardness of solving the learning-with-errors (LWE) problem over module lattices. Thus, the keys are slightly larger with comparable security and a side-channel attack is known [34]. Besides the ring-LWE and lattice-based approach, further promising approaches for POC are considered: multivariant polynomial, code-based, hash-based, and supersingular isogeny EC. Of these, the EC approach offers the most promising potential in terms of lightweight Cryptography. The key length in EC and supersingular isogeny EC cryptography is significantly smaller than in the other cryptosystems.

In the following, a retrospective of the development of supersingular isogeny EC cryptography is given:

– 1996 Couveignes [35] first mentioned about isogenies in cryptography.

– 2010 Rostovtsev and Stolbunov [36] presented first published isogeny-based public-key cryptosystem based on isogenies between ordinary curves.

– 2011 Jao and De Feo [37] presented the Supersingular Isogeny Diffie-Hellman (SIDH) [38].

– 2017 Jao et al. [39] proposed Supersingular Isogeny Key Encapsulaon (SIKE) as a submission to NIST PQC call.

The SIDH and SIKE approaches are the only known approaches based on supersingular isogeny. However, an active attack was found for SIDH [40,38]. This type of adaptive attacks is fundamentally prevented with our concept. Furthermore, the NIST calls for Lightweight Cryptography to protect small electronics, we are focus on [41].