WormHole Algorithm Outperforms BiBFS in Query Efficiency and Accuracy

Table of Links

Abstract and 1. Introduction

1.1 Our Contribution

1.2 Setting

1.3 The algorithm

2. Related Work

3. Algorithm

   3.1 The Structural Decomposition Phase

   3.2 The Routing Phase

   3.3 Variants of WormHole

4. Theoretical Analysis

   4.1 Preliminaries

   4.2 Sublinearity of Inner Ring

   4.3 Approximation Error

   4.4 Query Complexity

5. Experimental Results

   5.1 WormHole𝐸, WormHole𝐻 and BiBFS

   5.2 Comparison with index-based methods

   5.3 WormHole as a primitive: WormHole𝑀

References

5 EXPERIMENTAL RESULTS

In this section, we experimentally evaluate the performance of our algorithm. We look at several metrics to evaluate performance in different aspects. We compare with BiBFS, a traversal-based approach, and with the indexing algorithms PLL and MLL. We test several aspects, summarized next. Detailed results are provided in the rest of this section.

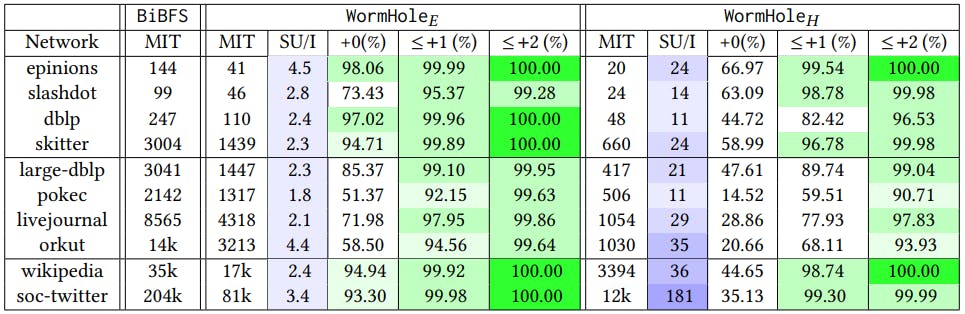
(1) Query cost: By query cost, we refer to the number of vertices queried by WormHole, consistent with our access model (see §1.2). We show that WormHole actually does remarkably well in terms of query cost, seeing a small fraction of the whole graph even for several thousands of shortest path inquiries. See Figures 2(b) and 5.

(2) Inquiry time: We demonstrate that WormHole𝐸 achieves consistent speedups over traditional BiBFS, even while using it as the sole primitive in the procedure. More complex methods such as PLL and MLL time out for the majority of large graphs. We also provide variants that achieve substantially higher speedups. Finally, in §5.3, we show how using the existing indexing-based state or the art methods on the core lets us achieve indexing-level inquiry times. See Figure 1.

(3) Accuracy: We show that our estimated shortest paths are accurate up to an additive error 2 on 99% of the inquiries for the default version WormHole𝐸; a faster heuristic, WormHole𝐻 , shows lower accuracy, but still over 90% of inquiries satisfy this condition. See §5.1 and Table 3 for details.

(4) Setup: We look at the setup time and disk space with each associated method. Perhaps as expected, WormHole𝐸 beats the indexing based algorithms by a wide margin in terms of both space and time: see Figure 7. In §5.3 we further show that using these methods restricted to Cin results in a variant WormHole𝑀 with much lower setup cost ( Table 6).

Datasets. The experiments have been carried out on a series of datasets of varying sizes, as detailed in Table 2. The datasets have been taken either from the SNAP large networks database [36] or the KONECT project [34]. We organize the results into two broad sections: we first introduce two variants

of our algorithm. We then compare it with BiBFS as well as indexing based methods – PLL and MLL. The latter two did not terminate in 12 hours for most of the graphs, while BiBFS completed on even our largest networks.

We classify the examined graphs into three different classes and use a fixed percentage as the ‘optimal’ inner ring size for graphs of comparable size (where the inner core size as % of the total size decreases for larger networks, an indication for the sublinearity of our approach). This takes into account the tradeoff between accuracy and the query/memory costs incurred by a larger inner ring. The classification is summarized in Table 1. For the experimental section, we default to these sizes unless mentioned otherwise.

Implementation details. We run our experiments on an AWS ec2 instance with 32 AMD EPYC™ 7R32 vCPUs and 64GB of RAM. The code is written in C++ and is available in the supplementary material as a zipped folder, with links to the datasets. The backbone of the graph algorithms is a subgraph counting library that uses compressed sparse representations [45].